初めに
記事の構成
- 添付文書や医療データを「正しく読み解く力」を身につけることができる
- 確率変数や確率分布の基本をわかりやすく学び、統計への苦手意識を克服できる
- 各種検定や区間推定を理解するために必要な「数学の基礎」をしっかり押さえられる
- 統計データを実務で役立てる具体的なヒントや考え方を学べる
医療データへの応用例
そのデータ信頼性は?
添付文書には、臨床試験で測定されたさまざまなデータが記載されています。しかし、これらは全ての患者を調査したわけではなく、試験対象として抽出されたサンプル集団のデータです。統計的な手法を用いることで、このサンプル集団のデータから元となる母集団の特徴を推測することができます。この手法を「推測統計学」と呼びます。
推測統計についていくつか具体例に触れてみます。
治療効果を見極める!帰無仮説と二項分布のはなし
ある新しい薬を咽頭炎患者4名に投与したところ、4名中3名が1週間以内に症状が改善しました。一方で、未治療の場合の1週間以内の症状改善率は50%であることがわかっているとします。すると、「この薬、本当に効果があるの?」という疑問が湧きますよね。
なぜなら、「薬には効果がなくても、たまたま4名中3名が1週間以内に症状が改善した」という偶然の可能性も否定できないからです。
そこで、「薬に効果がない」という前提(帰無仮説)のもと、4名の患者について「0人が改善する場合」「1人が改善する場合」「2人が改善する場合」……といった全てのパターンを考え、それぞれのパターンになり得る確率を計算します。
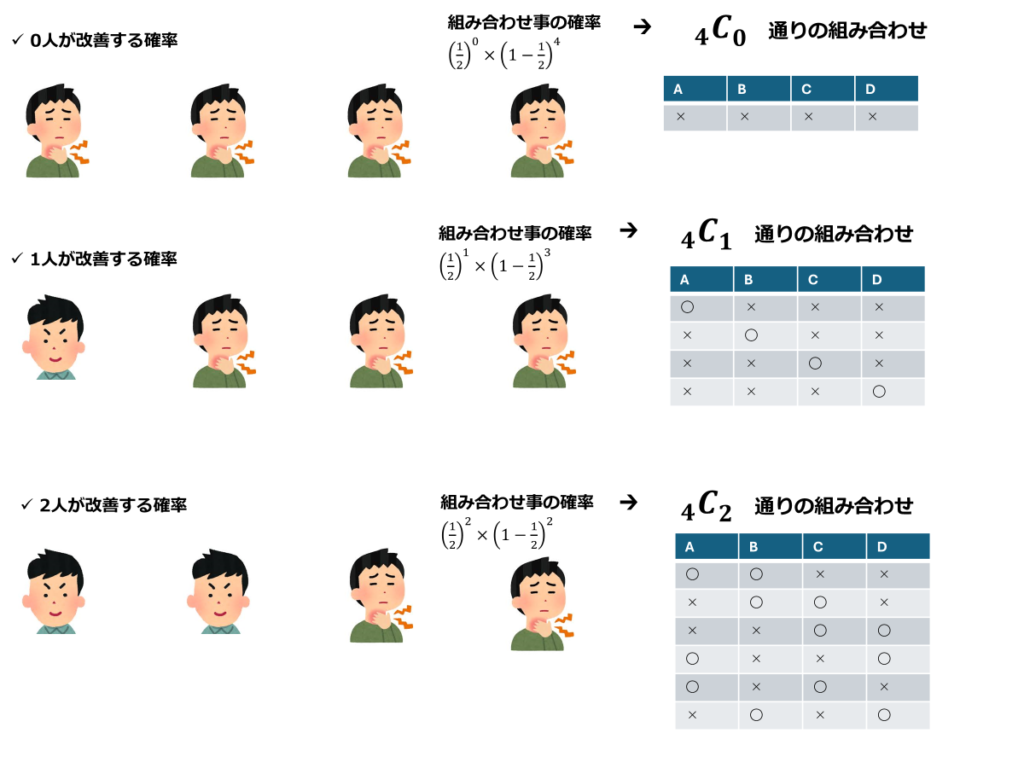
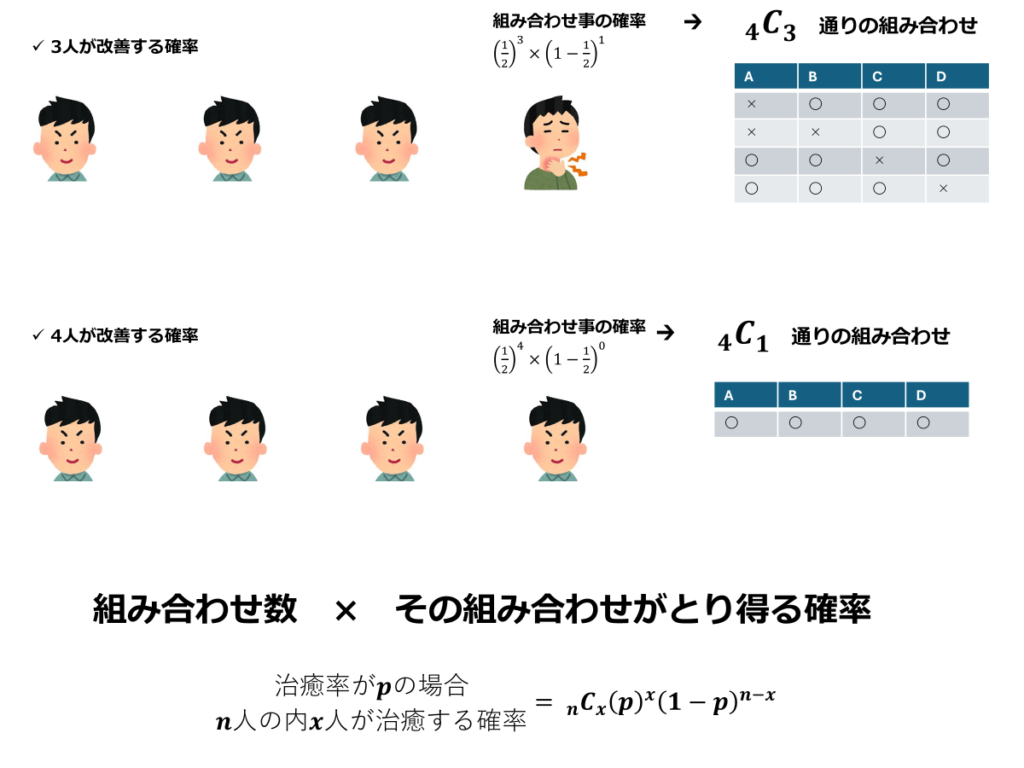
各組み合わせごとに、発生する確率を計算していきます。このように、確率pの事象をn回繰り返したとき、その発生数が従う分布を二項分布といいます。

最初に述べたように「薬には効果がなくても、たまたま4名中3名が1週間以内に症状が改善した」という偶然の可能性を考えます。
この場合、4人中3人が改善する確率は0.25(4/16)、4人中全員が改善する確率は0.0625(1/16)となります。これらを合計すると0.312になります。
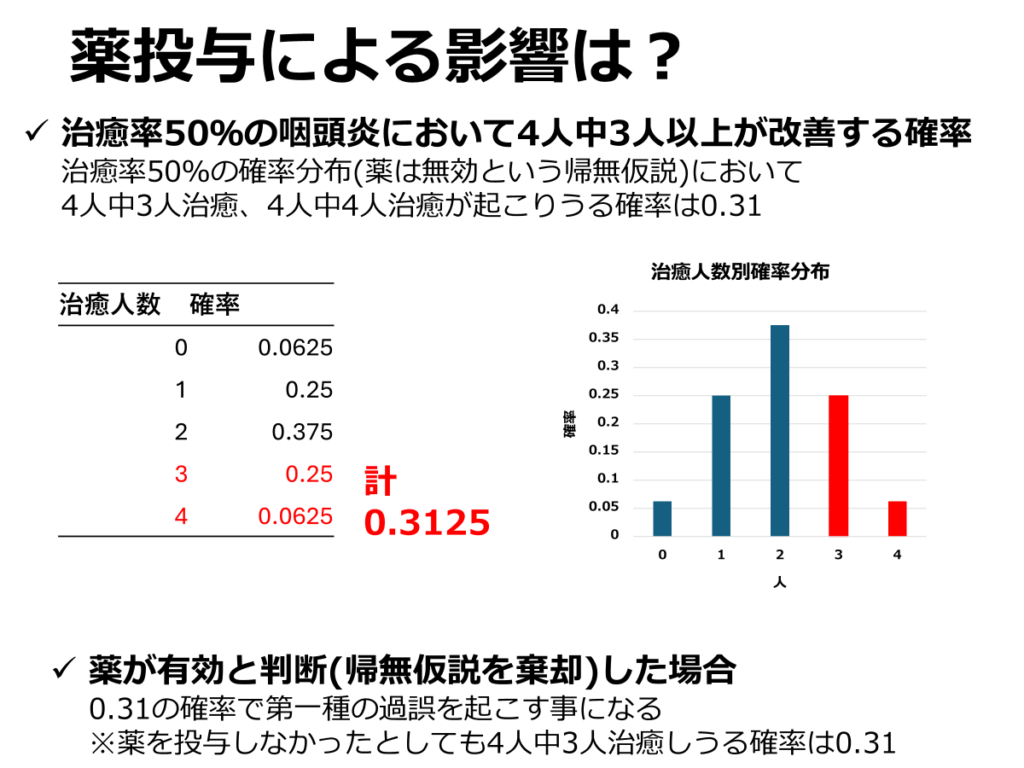
つまり、薬に効果がなかったとしても、約31.2%の確率で4人中3人が改善する結果が得られる可能性があると解釈できます。
この確率(今回の場合は0.31)は、推測統計においてp値として扱われます。
統計的仮説検定において、帰無仮説の元で検定統計量がその値となる確率のこと。P値が小さいほど、検定統計量がその値となることはあまり起こりえないことを意味する。
一般的にP値が5%または1%以下の場合に帰無仮説を偽として棄却し、対立仮説を採択する。
一般的に、データの例数が増えても同じ比率の結果が得られる場合、p値は小さくなっていきます。そこで、「4人中3名以上改善」という比率を保ちながら、「8人中6名以上改善」「12人中9名以上改善」「16人中12名以上改善」の場合について考えてみましょう。
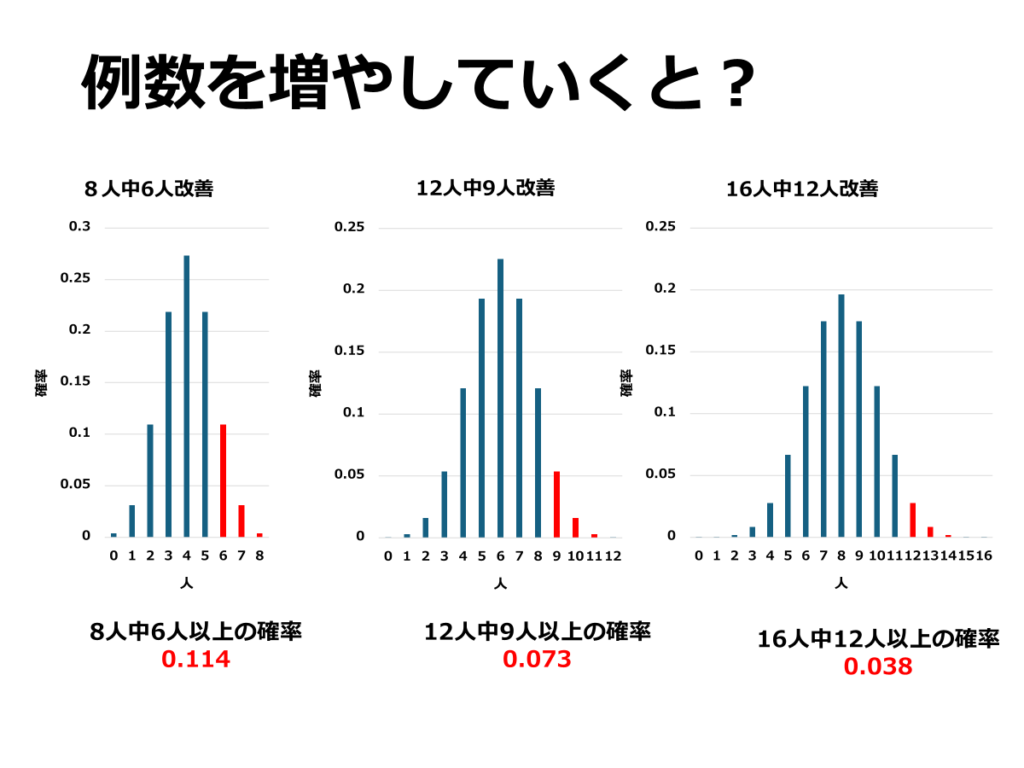
結果として、p値はそれぞれ0.114、0.073、0.038と徐々に小さくなることが分かります。
統計では、p値がどの程度まで許容されるかを有意水準と呼び、一般的には0.05以下で「有意差がある」と判断されます。今回の薬の事例では、16人以上の患者で同様の結果が得られれば、有意差があると判断できるというわけです。
今回の推定では、サンプル4例のデータをもとに、より大きな人数で起こり得る確率を推定しました。このような手法を母集団推定と呼びます。また、サンプルの結果から母集団でも差があるかどうかを検証する手法を仮説検定、母集団における結果の範囲を推定する手法を区間推定といいます。
補足 区間推定の例
上記の仮説検定では、「薬物Aによって咽頭炎の有効率が上昇する」という前提を基にしているため、改善が多くなる場合(上側の確率)のみを考慮しました。たとえば、「4人中3人以上が改善する確率」を求めて、薬の効果を検証しました。
一方で、区間推定では「薬物Aに効果がない場合、咽頭炎が1週間以内に改善する人数がどのように分布するか」を推定します。そのため、改善が少ない場合(たとえば4人中0人や1人が改善する確率)も含め、全体の分布を考慮する必要があります。このように、区間推定では上側と下側の確率の両方を扱う点が特徴です。
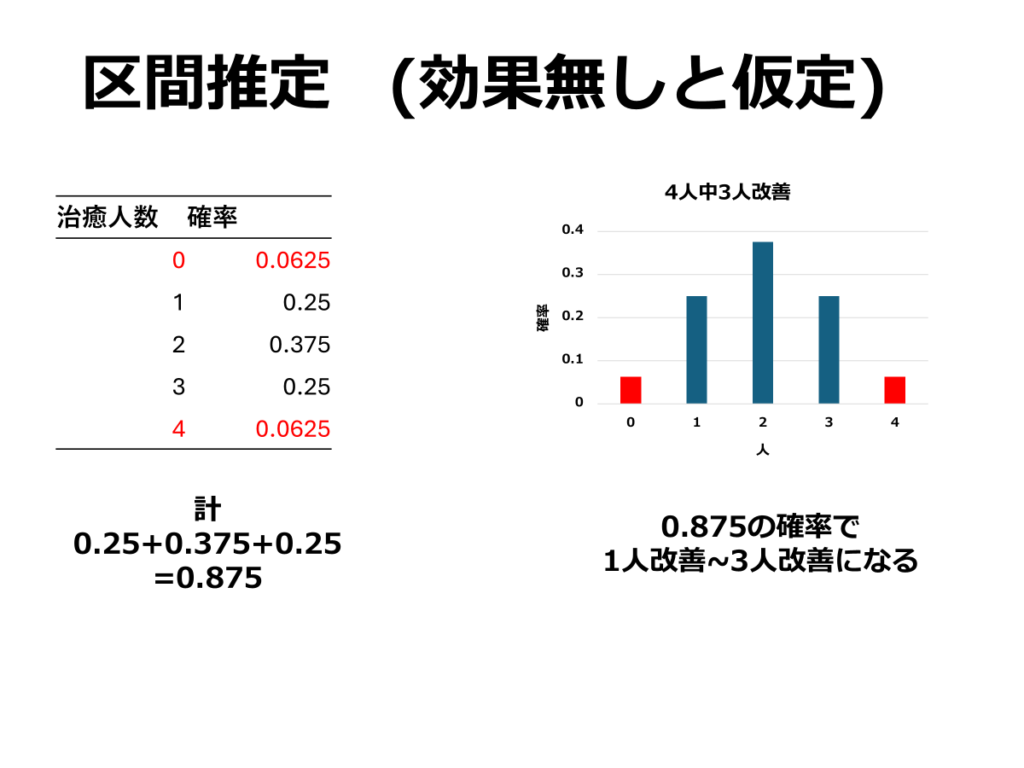
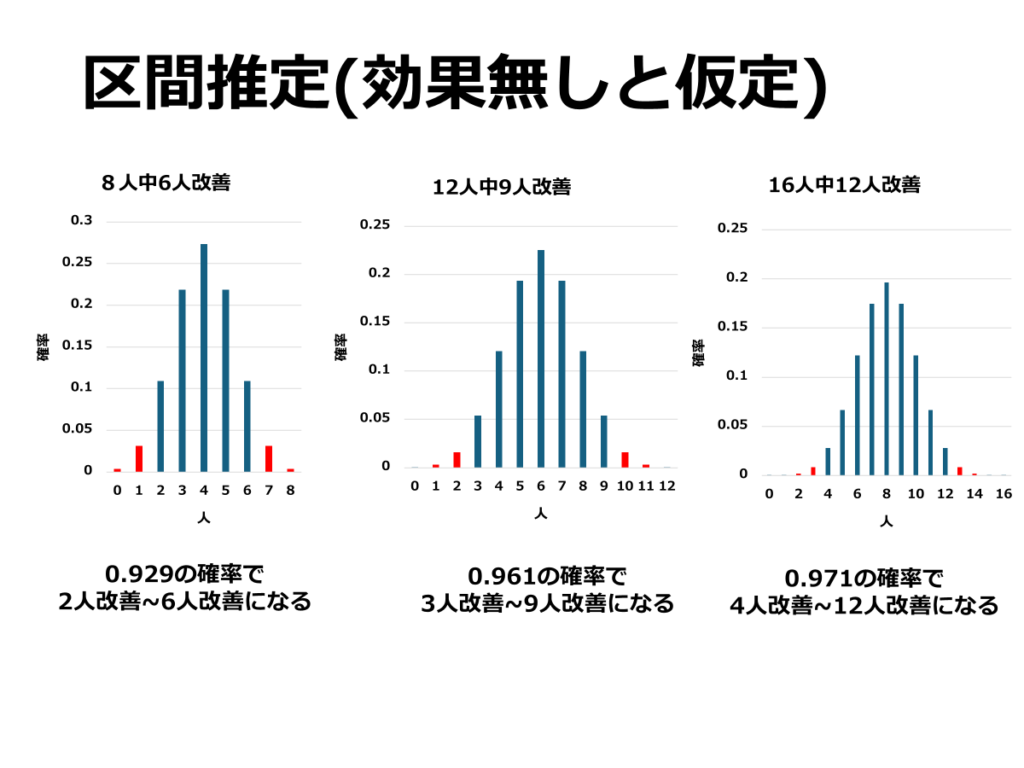
同じ確率でも、群数を増やしていく事で信頼度が上がっていきます。
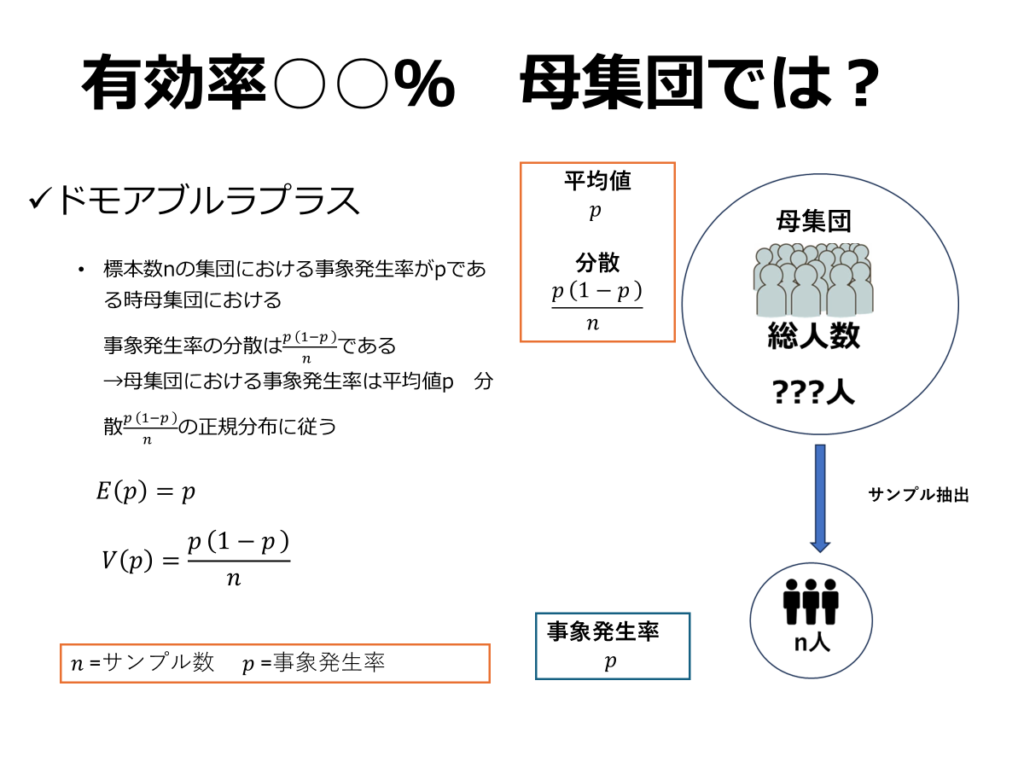
ドモアブル-ラプラス式で比率の推定を
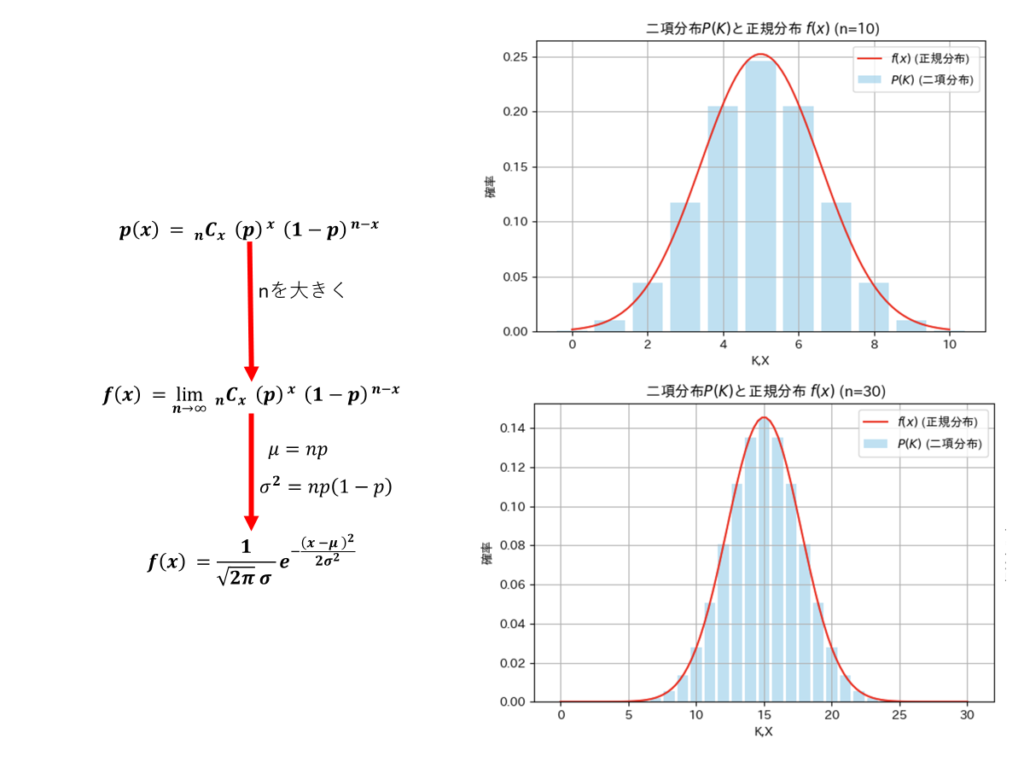
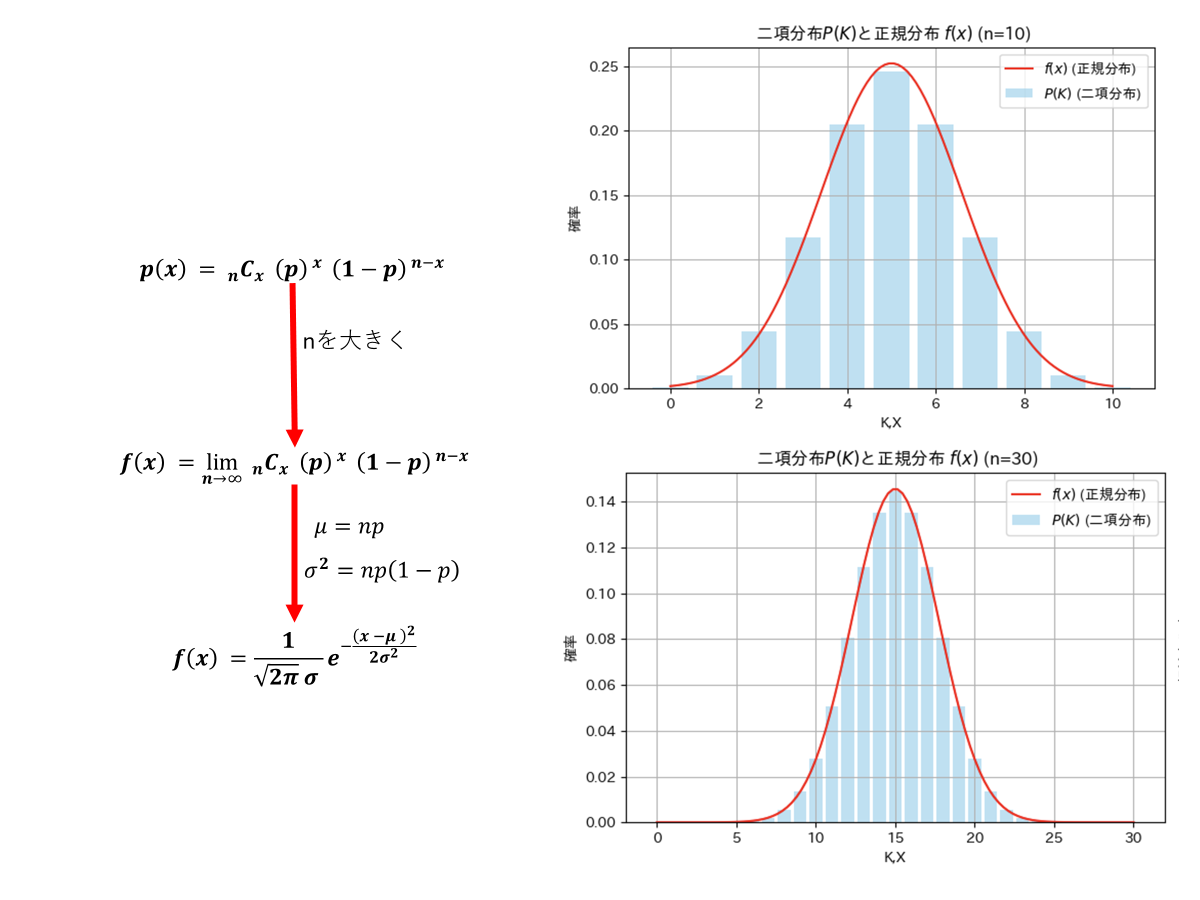
標本数が十分に大きい場合に限り、ド・モアブル・ラプラスの定理を用いて母集団の区間推定を行うことができます。この定理は、試行数nと成功確率pの二項分布について、標本数nが増加するにつれて、その分布が正規分布に近似できるというものです。具体的には、期待値がnp、分散がnp(1-p)を持つ正規分布に収束します。
以下は、成功確率p=0.5の二項分布について、試行回数n=10およびn=30の場合の分布を示し、それぞれにド・モアブル・ラプラスの式で推定した正規分布を重ねてプロットした図です。
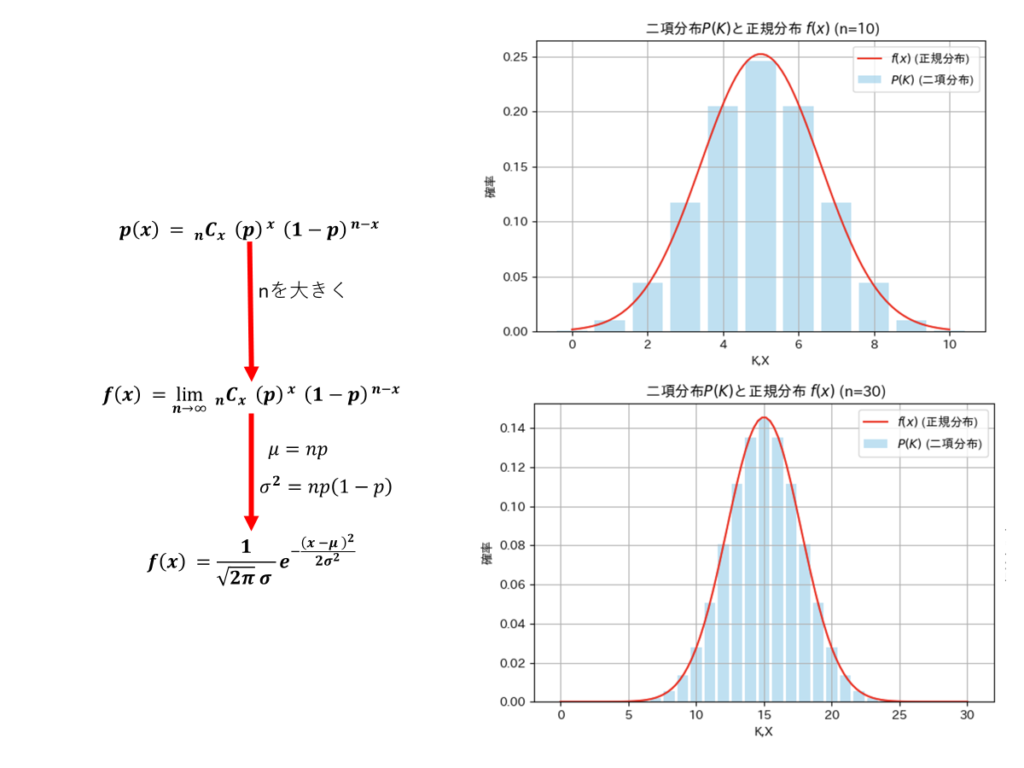
n=10では、二項分布の棒グラフがまだ階段状に見え、正規分布の曲線と完全には一致していません。一方、n=30では、二項分布の形状が正規分布に非常に近づき、ほぼ重なっている様子が確認できます。この結果から、標本数nが増えることで二項分布が正規分布に収束する性質が視覚的に示されています。

今回の具体例として、オーグメンチン配合錠の添付文書より引用した、耐性菌が検出された慢性気管支炎症例における有効率。こちらの確率と症例数を基に95%信頼区間の算出を行ってみたいと思います。
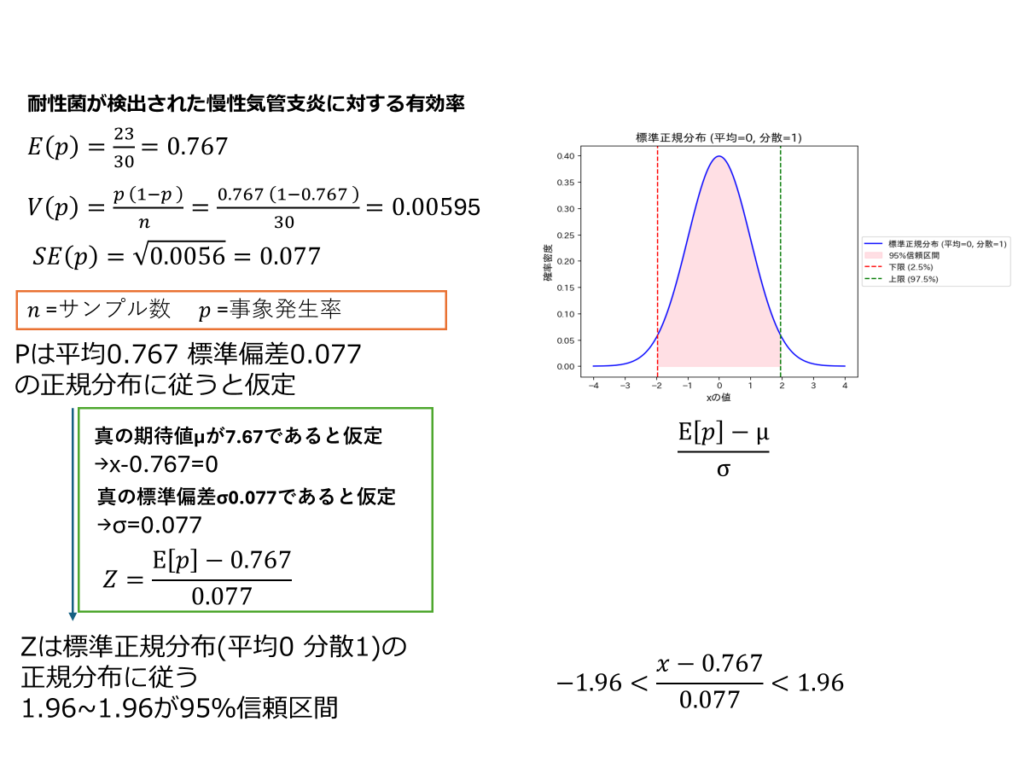
ドモアブルラプラス式で平均と分散を算出した後、真の分布が標準正規分布に従うと仮定して区間推定を行います。この区間推定では、前述と同様に両側確率を基に計算を行っています。

標準正規分布とは、平均が0、標準偏差が1の正規分布を指します。任意の正規分布の確率変数について、その値から平均を引き、標準偏差で割ることで標準正規分布に従う値(標準化変数)を得ることができます。この標準化により、異なる正規分布を統一的な基準で扱えるようになります。
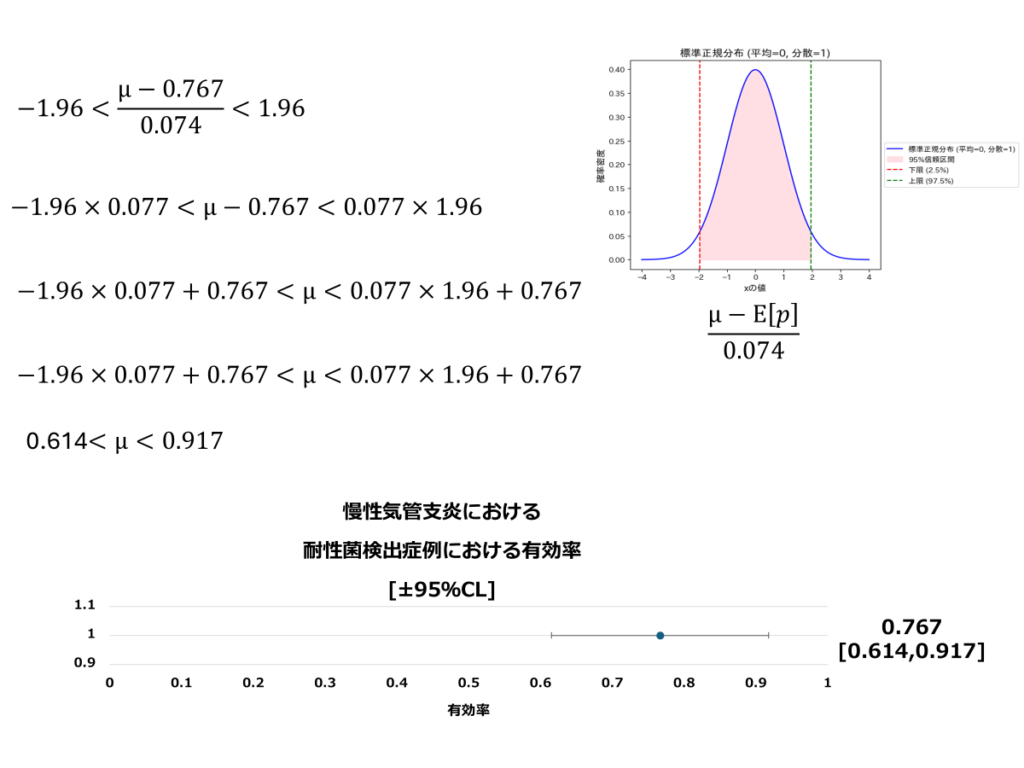
計算結果から、耐性菌検出した慢性気管支炎に対するオーグメンチン配合錠の有効性は95%の確率で0.614~0.917にあると解釈出来ます。
T分布を活用しサンプル集団のデータから母集団における薬物動態を推測!
データが連続値で、なおかつ標本数が少ない場合には、T分布を活用して母集団の特性を推測します。T分布は、標本数が少ない状況でも信頼性の高い推定を行うために用いられる分布です。
降圧薬として広く使用されているテルミサルタンの血中濃度を例にとってみましょう。以下にT分布の式と添付文書に記載されている繰り返し投与時の薬物動態パラメータを記します。
反復投与時最高血中濃度の95%信頼区間

サンプル集団における反復投与時の最高血中濃度データを基に、母集団がとり得る最高血中濃度平均値を推測してみます。今回は母集団の分散が未知であるためT分布を用いて推測します。
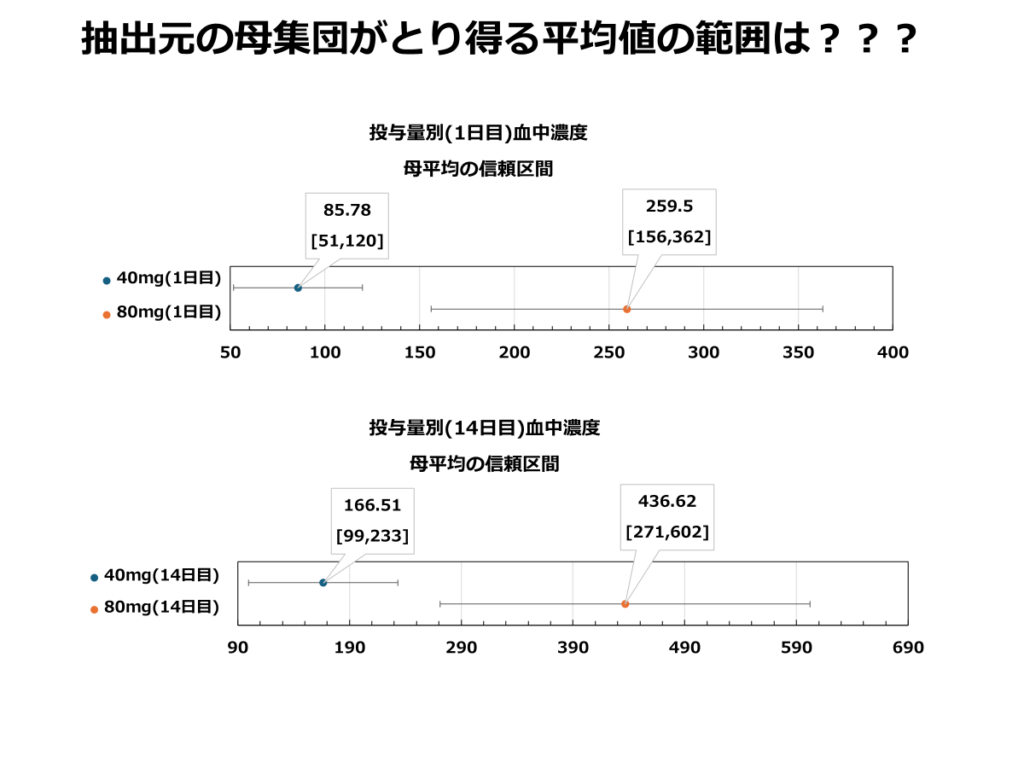
添付文書に記載されているサンプル集団のデータを基に、母集団における平均値の95%信頼区間を算出してみました。この信頼区間は、「95%の確率で母集団の平均値がこの区間内に含まれる」と解釈することができます。
95%信頼区間算出の計算過程
以下は、40mg投与1日目のデータを基に、95%信頼区間を算出した例です。添付文書に記載されている平均値(85.78 ng/ml)、標準偏差(45.25 ng/ml)、サンプル数(10人)を使用し、普遍分散及び自由度、T統計量を算出して母平均の区間推定を行いました。

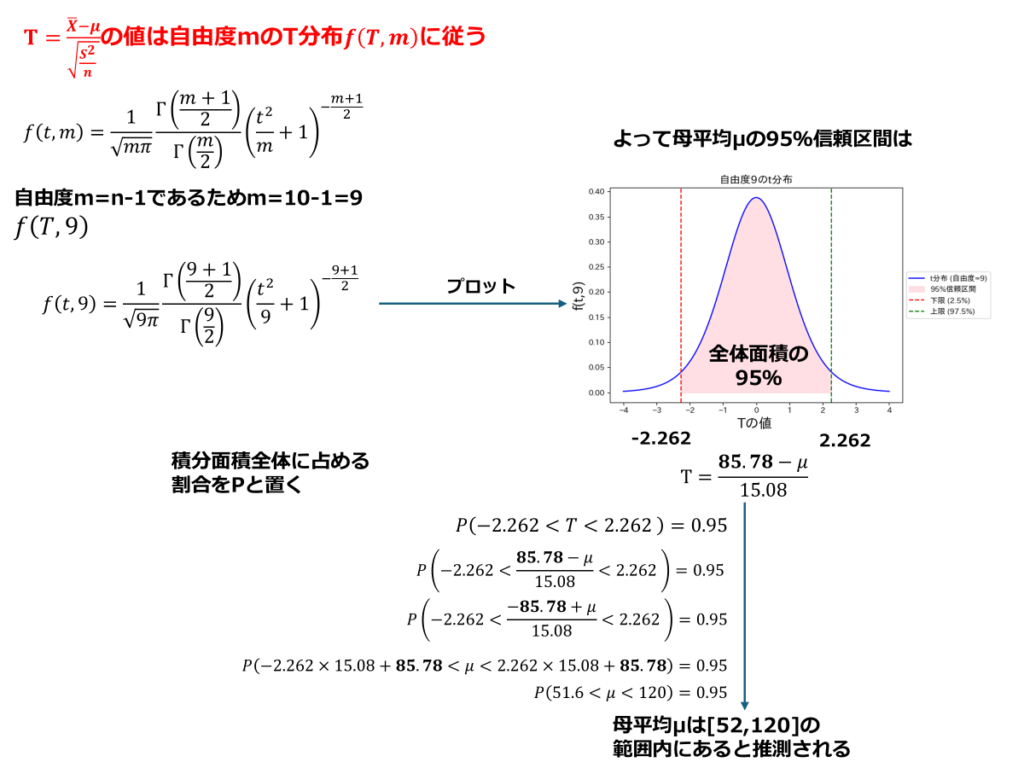
結果、95%の確率で血中濃度は52ng/ml~120ng/mlの間にあると解釈する事が出来ます。
母集団推定のメカニズムを理解する為に?
※ドモアブルラプラス式


※T統計量とT分布の確率密度関数(鹿児島大学 公開資料より)
発現率で取り扱ったドモアブル-ラプラスの式や、テルミサルタン血中濃度推定で用いたT統計量、T分布などは、数学や確率論を基に導き出されたものです。統計の基礎となる数学をしっかり理解することで、「母集団における事象発生率の分散が何故p(1-p)/nなのか?」「母分散が未知の状態で、なぜT分布を用いた推測が可能なのか?」といった疑問を解消できます。
https://www.eee.kagoshima-u.ac.jp/~watanabe-lab/misc/t%E5%88%86%E5%B8%83.pdf鹿児島大学 公開資料より引用
これを理解するには、確率変数の性質や確率密度関数、そして微分積分の知識が欠かせません。そこで、次項からはこれらの基礎知識を順を追って解説していきます。
今回は特に「確率変数」と「確率分布」を中心に取り上げ、それ以外の内容については続編で詳しく触れる予定です。
確率変数と確率分布の基礎
離散分布と連続分布
確率分布は大きく「離散分布」と「連続分布」に分類されます。代表的な例として、離散分布には二項分布、連続分布には正規分布があります。
二項分布において、試行回数(サンプル数)nを増やすと、取り得る成功回数の分布が滑らかになり、正規分布に近づいていきます。
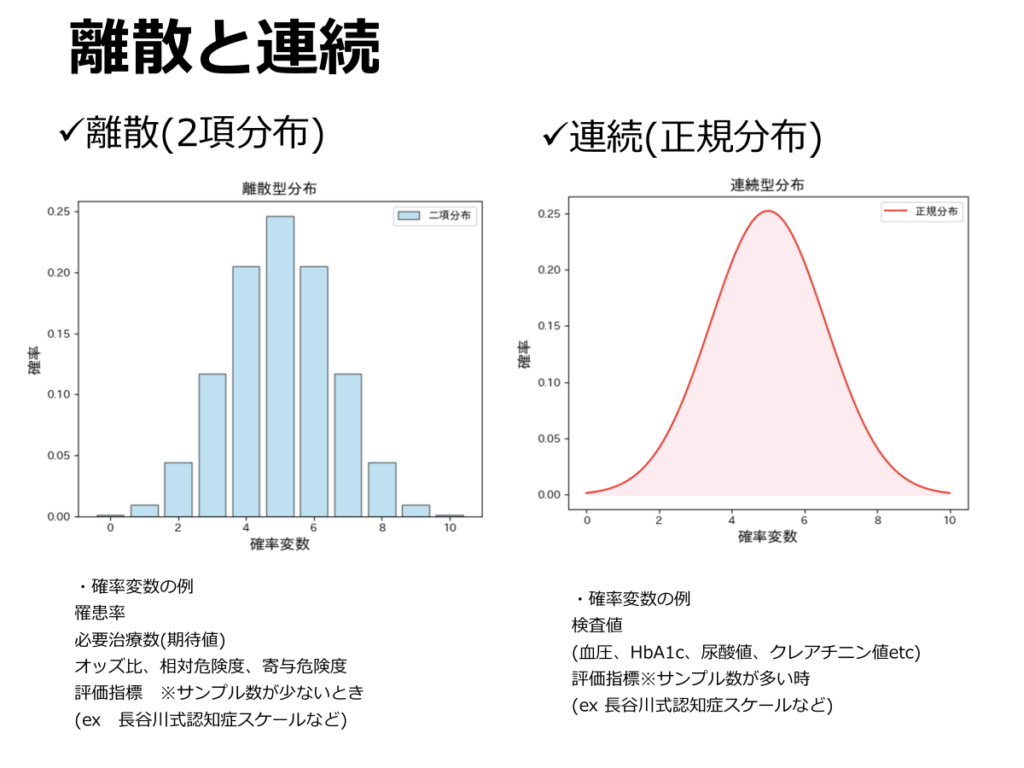
離散型確率変数の例としては、罹患率、必要治療数(NNT)、オッズ比、相対危険度(RR)、寄与危険度(AR)などが挙げられます。一方、連続型確率変数の例には、身長、体重、血圧、HbA1c、尿酸値、クレアチニン値、血中薬物濃度などがあります。
正規分布と二項分布の確率密度関数
確率分布を考える上で重要な概念に確率密度関数(PDF: Probability Density Function)があります。確率密度関数は、X軸に確率変数、Y軸にその確率変数が取り得る値の「確率の大きさ」をプロットしたものです。
※二項分布の確率密度関数
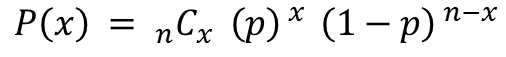
※正規分布の確率密度関数
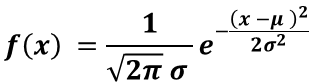
離散型確率密度関数では、Y軸の値をそのまま確率として解釈できます。たとえば、サイコロを振った場合に特定の目が出る確率(1/6)は、この確率密度関数の一部です。一方で、連続型確率密度関数では、Y軸の値そのものは「密度」を表し、確率として解釈するには、特定の範囲における積分(面積)を計算する必要があります。たとえば、身長が160cmから170cmの間に収まる確率は、この範囲の面積として求められます。
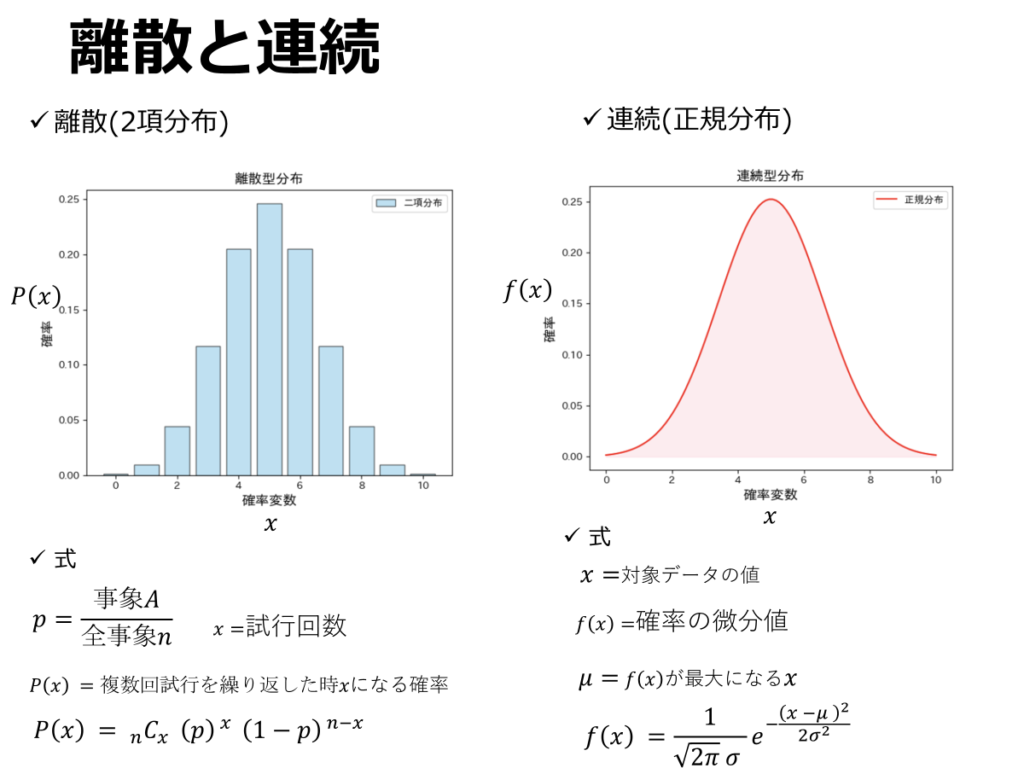
確率密度関数には、重要な性質があります。それは、確率の総和や無限範囲における積分が必ず1になるということです。
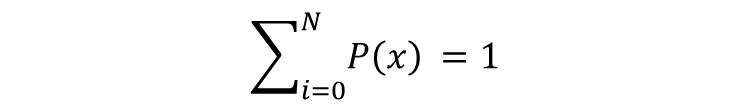
離散型確率変数の場合、すべての値に対応する確率を足し合わせた総和が1になります。たとえば、サイコロの目の確率では、1/6 × 6 = 1 となります。
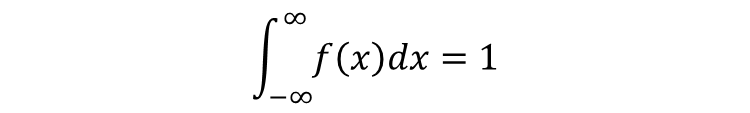
一方、連続型確率変数の場合は、確率密度関数の曲線の下の面積を無限範囲で積分すると1になります。これは、連続分布において確率密度そのものを直接測るのではなく、範囲での面積を確率として解釈するためです。この性質により、どの確率変数でも全体の確率が常に100%になるよう保証されています。
まとめ
今回の記事では、添付文書等に記載されたデータを基に統計的に評価を行う手法や考え方について触れました。今後の記事でこれらの計算を行う為の基礎知識である期待値や分散の性質、そして各分布の確率密度関数について触れていく予定です。
期待値や分散の性質を理解する事で、二群間の差の検定や区間推定等にも応用していく事が出来ます。また、複数の薬剤の添付文書情報を基に有意差検定を行う事なども可能になります。
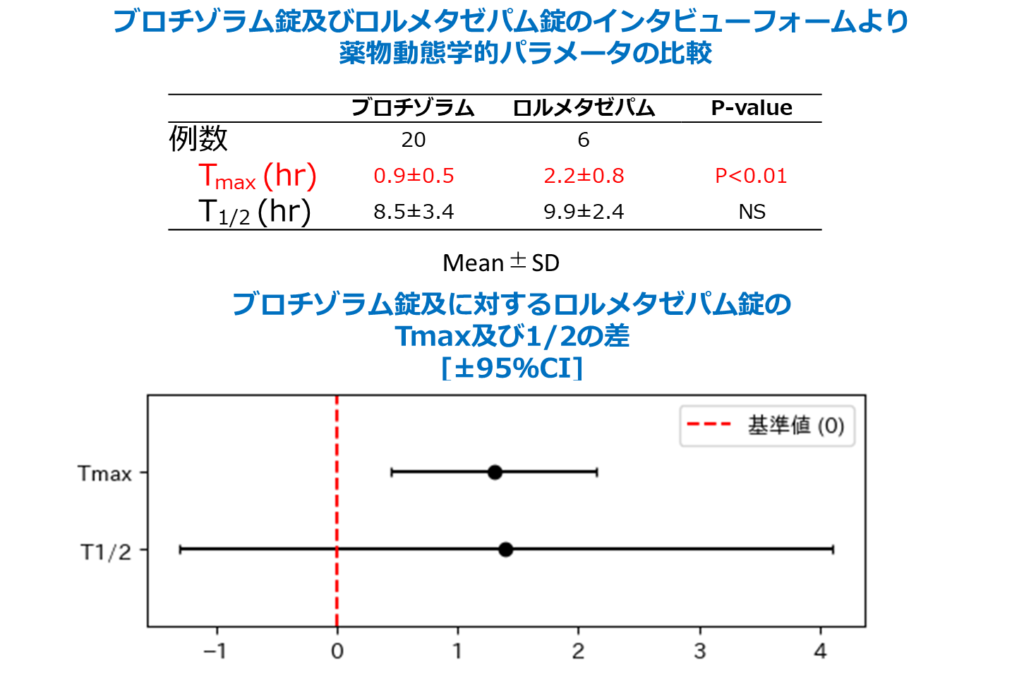
以下に、二種類の睡眠薬の添付文書に記載された薬物動態パラメータ及び副作用発現率の期待値、分散、サンプル数を基に統計的に比較したデータを示します。
※睡眠薬の薬物動態パラメータ比較(引用禁止でお願い致します)
→最高血中濃度、半減期の平均値・分散・サンプル数を基に2群間T検定を実施、差の母平均の信頼区間を算出
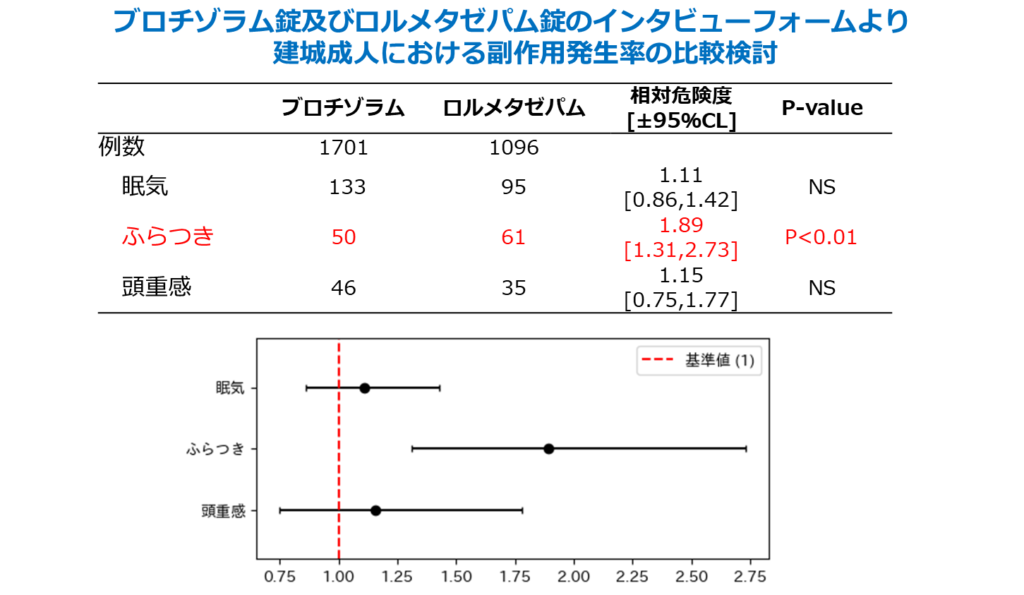
※睡眠薬の薬物動態パラメータ比較(引用禁止でお願い致します)
→臨床試験時における副作用発生件数、サンプル数を基に2項検定を実施、相対危険度を算出し区間推定。
また、確率密度関数の成り立ちを理解する事で、先ほど取り扱った二項分布の正規近似、T分布の確率計算などもより深く理解する事が可能になります。
- 統計の基本は帰無仮説に基づく分布に基づいて行う
- p値とは、帰無仮説の分布において観測された事象がどの程度の確率で起こり得るかの値
- 確率分布は大きく分けて離散分布と連続分布がある
- 離散型確率密度関数の総和、連続型確率密度関数の無限範囲積分値は必ず1になる(全事象)
- 確率密度関数の性質を用いる事により分布内での事象発生割合を算出する事が出来る。






コメント