こちらの記事では、統計学的検定を行う上で非常に重要なデータの種類と特徴について掘り下げてご説明させて頂きます。本編は全編にあたる医療統計の勉強を始めるにあたり知っておきたいこと。(統計の勉強法・目的)の続編にあたります。
統計学の全体像と各学習項目のまとめになりますので、こちらを見ていない方はこちらからお読み下さい。
[hoops name=”test”]
対象読者
- 前回の記事をお読み頂いた方
- 研究や実務実習などで論文を読む機会がある薬学部4~6年生。
- 数学が苦手な薬学生、薬学部入学予定の高校生
- 統計をしっかり理解したい薬学生
データの種類について
今回の記事では、統計分析で取り扱う事になるデータの種類、特性を説明させて頂きます。仮説検定で行われる計算処理の流れについてそれぞれご説明させて頂き、その流れで必要にされるパラメータ(比率、平均、順位)などの観点から適切な検定の選択方法に繋げていきたいと思います。
統計処理の流れからデータに適した検定方法を紹介する事が今回のメインテーマです。数式や確率関数等が一部登場しますが、現段階では細かい導出などには触れず、どの様に式が用いられているかの説明に留めております。
今後、各検定手法の詳細について別記事を作成していく予定ですのでそちらで詳しい内容に触れていく予定です!
分析におけるデータの取り扱い方法
カテゴリデータと数値データ、正規分布性の有無
概要(カテゴリ、数値)
検定の選択方法で非常に重要になるのは以下の二つの観点になります。それはデータの連続性の有無と平均値の信頼性になります
- データの連続性の有無
→非連続データか連続データか? - (連続データの場合)データの平均値の信頼性
→平均値を使えるか使えないか?
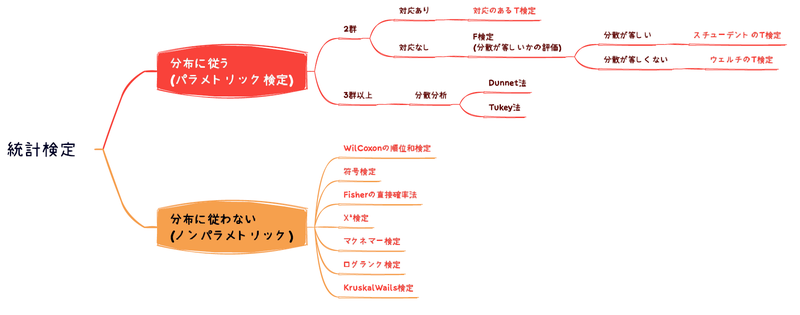
データの性質に応じて、比率、平均値、順位のいずれかのパラメータを用いて検定手法を選択することになります。
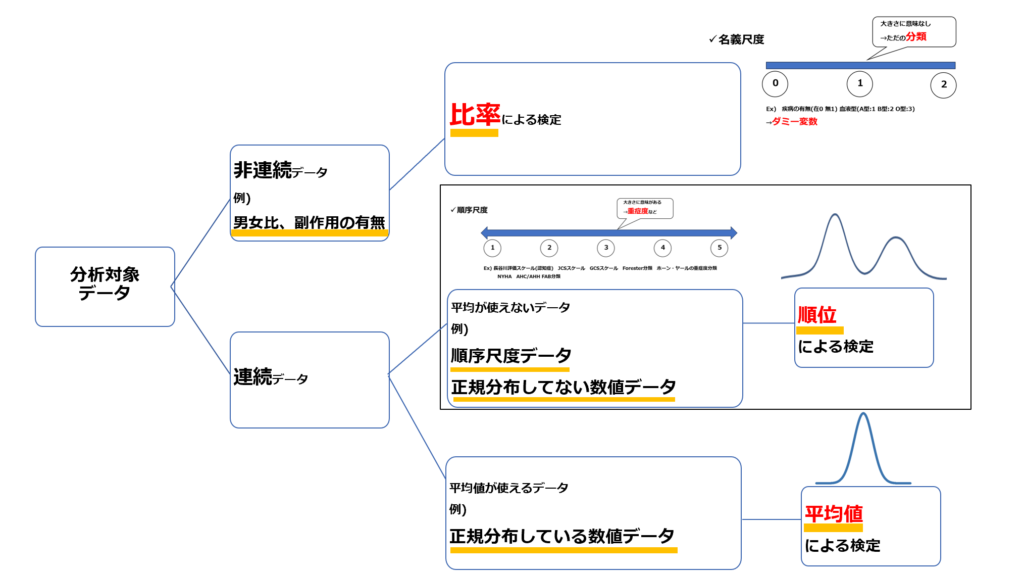
後述しますが、検定手法は以下のように使い分けます
また、平均値の使えない検定の事をノンパラメトリック検定、対して平均値の使える(正規分布性のある)検定の事をパラメトリック検定と呼びます。
| 検定対象 | 具体例 |
|---|---|
| 比率による検定(ノンパラメトリック) | ・カイ二乗検定 →サンプル数が多い時 ・Fisher検定 →サンプル数が少ない(5以下のマスがある)時 ・ロジスティック回帰分析 |
| 順位による検定(ノンパラメトリック) | ・マンホイットニーのU検定 ・クラスカルウォリス検定 |
| 平均値による検定(パラメトリック) | ・T検定 ・分散分析 ・相関分析 ・回帰分析(単回帰、重回帰) |
順序性のないデータ(男女比、副作用の有無)の場合
比率による統計処理を考える(ノンパラメトリック)
原則として、名義尺度のカテゴリデータでは数字の大きさそのものに意味はありません。男女比、血液型、副作用の有無などで判別をするための識別子として番号を割り振っているだけです。このためこの数字をそのまま検定に使うことはできません。
この問題を解決する手段として、比率による検定を行います。全体のうち男女比はどれくらいか?血液型はそれぞれ何割ずついるか?投薬によって副作用の発現する人は何倍に増える(減る)か?などです。
これを用いた具体例がカイ二乗検定やFisher検定になります。
カイ二乗検定では、基本的に郡分けとアウトカムの有無などで2×2の表を作成します。
そして各マスの実測値と理論値(期待値)の差を基に検定統計量を算出します。そしてこの検定統計量が帰無仮説のカイ二乗分布に従うものとして検定が行われます。
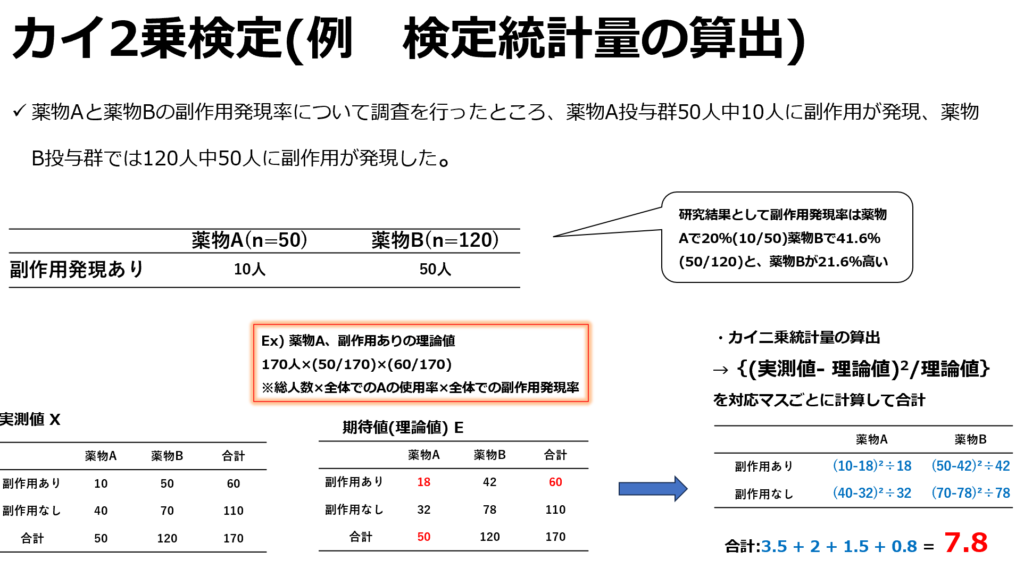
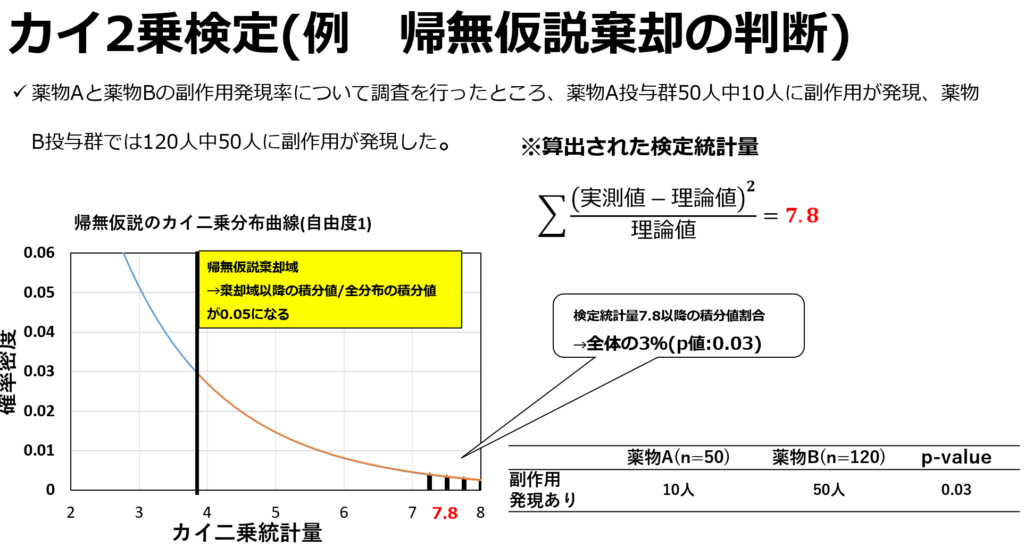
カイ二乗検定では下記の式により、統計量を算出しています。これは分母に期待値を含むため、サンプル数が少なく期待値が小さい値の場合、値が大きく算出され、p値が過小評価される事があります。原則として、期待値が5以下になる場合はカイ二乗検定は適していません。

このような時に用いられる検定手法がFisher検定になります。Fisher検定では、取り得る全ての組み合わせを考えます。そしてそれぞれの確率を算出し、実測値になる確率と実測値よりも大きな差が見込まれる確率からp値を算出します。
考えられる組み合わせにおける確率を全て検討するため、例数が少ない場合でも正確に検定を行う事が出来ます。
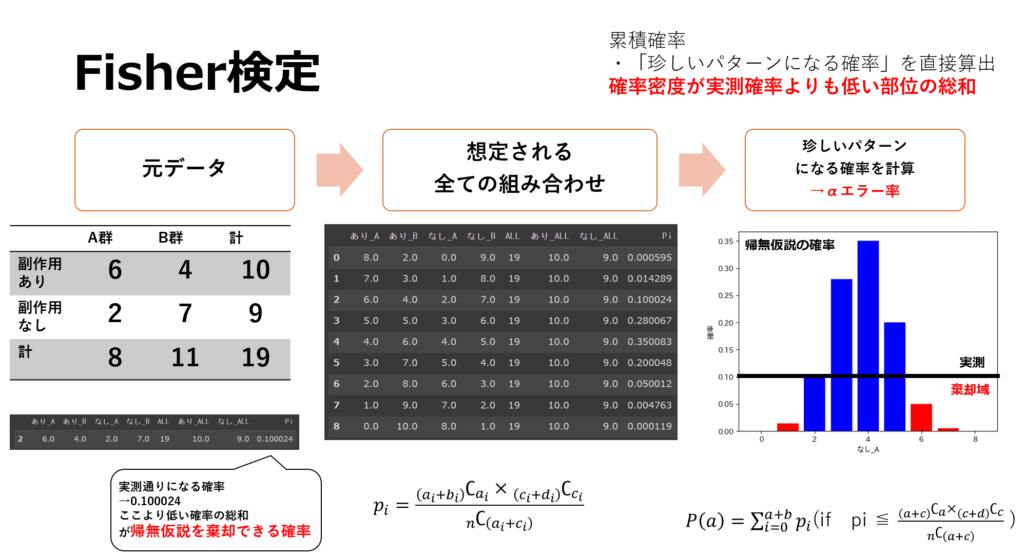
組み合わせの確率計算を行う影響で、逆に例数が多かったりすると計算に時間がかかる、ある程度高性能な統計ソフトでなければ計算できないなどのデメリットがあります。
※Excelでは500例程度までが限界でした。
| 検定方法 | メリット | デメリット |
|---|---|---|
| カイ二乗検定 | ・計算負荷が少ない | ・サンプル数が少ないと過小評価 |
| Fisher検定 | ・サンプル数が少なくても正確な評価が出来る。 | ・計算負荷が大きい →excelだと50例程度で限界 |
また、少し拡張的な概念として○○である確率は何割?といった解釈を行う事があります。その例として、ロジスティクス回帰分析があります。
例えば性別を目的変数としたロジスティク回帰分析では、説明変数の各因子から「男性(女性)」である確率は××割である。といった結果が得られます。これは回帰分析による母集団予測を行うときなどにに主に用いられます。
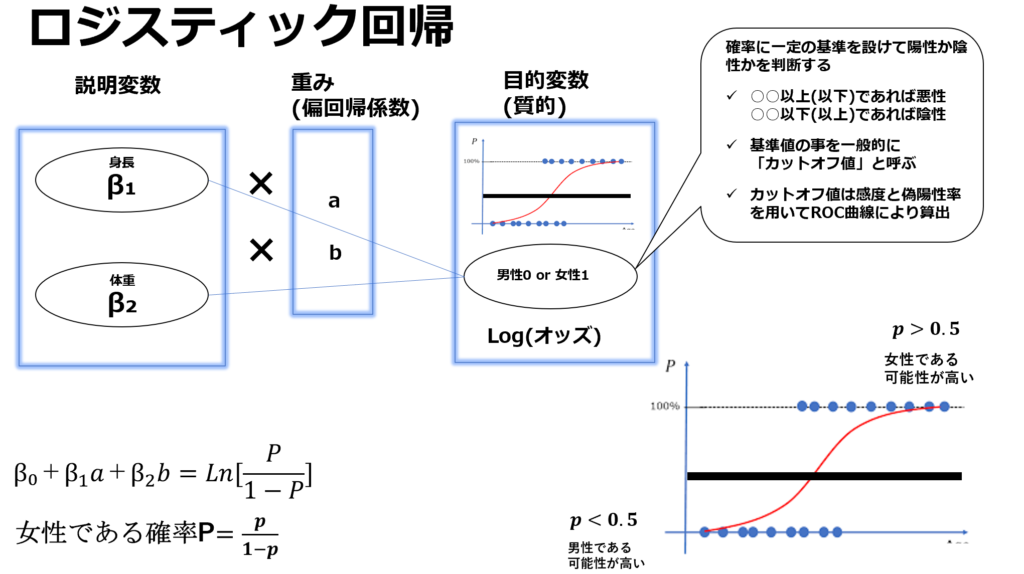
回帰により性別を予測したいとします。以前の記事からの引用になりますが、カテゴリ変数を直接数式で処理する事は出来ません。例えば、男性を0、女性を1として変数化した場合、回帰分析の出力結果によっては0.6と出力され・・・

性別どっちだよ!!!
となってしまいます・・・
このため、カテゴリ変数を直接的に回帰分析の目的変数とする事は不可能です。
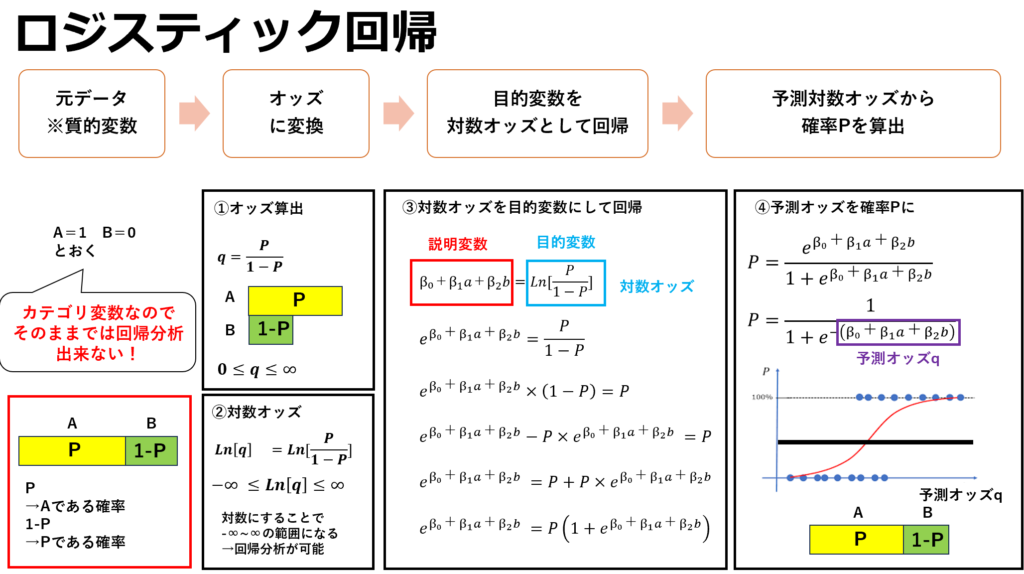
ロジスティクス回帰分析では対数オッズを目的変数として回帰予測する事により、男性である確率は○○%、女性である確率は××%といった形で予測する事が出来ます。
※対数オッズや細かい式変形、計算の流れなどは後日別記事でご紹介いたします。
順序性のあるデータであれば平均値の信頼性の有無を考える
そもそも平均値の信頼性とは?
順序性のあるデータにおける検定法を選択する際はまず最初に平均値の信頼性を考えます。ここで言う信頼性とは、「平均値がどの程度集団の状態を反映するか?」になります。平均値が信頼できない場合は順位による検定手法を選択することになります。
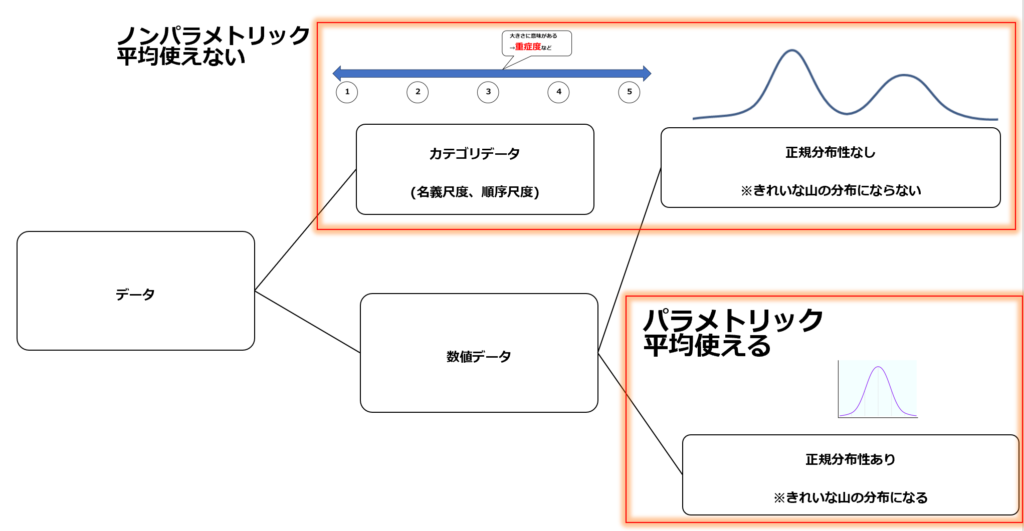
平均値が信頼できないデータは以下の2パターンがあります。
- 間隔尺度である
- 重症度分類で1~5まであるとします。平均値が3.5になりました。重症度3なのか4なのか判別する事が困難です。この場合平均値は信頼できないと言えます。
- 正規分布していないデータ
- クラスのテストの平均点が65点でした。でも実際は高得点層と赤点層に二極化しています。この場合65点という点数がクラスの状況を反映している訳ではありません。このような場合も平均点は信頼できないと言えます。
平均値が信頼できない場合は順位による統計処理(ノンパラメトリック)
平均値が信頼できないデータでは主に以下のようなノンパラメトリック検定が用いられてます。ノンパラメトリック検定で代表的なものがマンホイットニーのU検定であり、それを拡張し3群間比較を可能にしたものがクラスカルウォリス検定になります。
AクラスとBクラスでテストでの得点を比較したいとします。分布を箱ひげ図で可視化してみたところ以下のようなデータになりました。Aクラス、Bクラス共に中央値は同じあたり(65点付近)にありますが、分布が大きく異なっていることが推測されます。
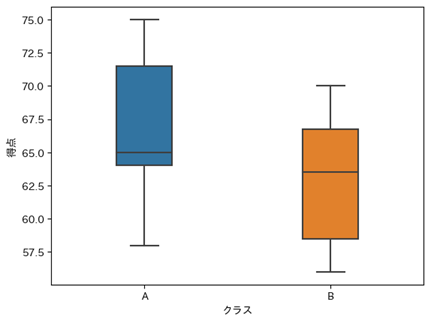
このようなデータの場合、平均値を算出しても、その値がクラス全体として見た時の得点分布を正確に反映しているとは言えません。
このような場合に用いられる検定がマンホイットニーのU検定(wilcoxonの順位和検定)になります。マンホイットニーのU検定ではデータの順位を指標として検定統計量を算出するためこのように平均値が信頼できない場合でも正確に検定を行う事が出来ます。
以下が検定の流れと計算方法になります。
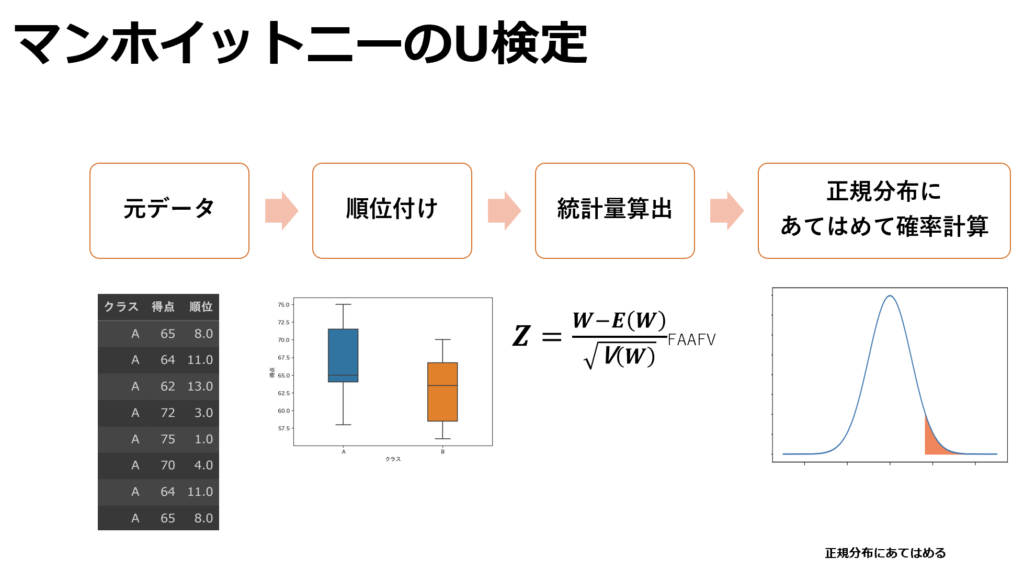
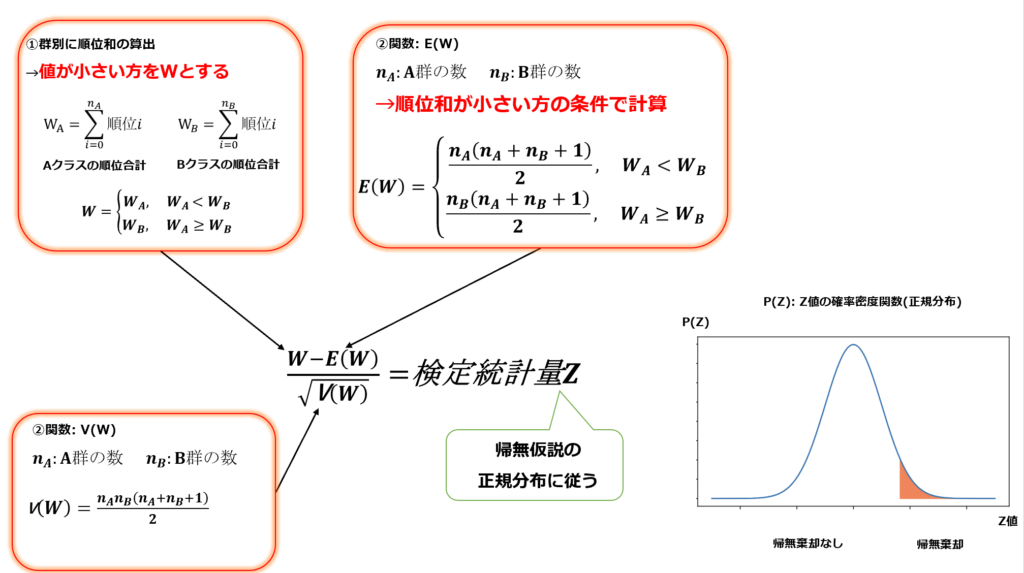
数式が多いので以下に要点を示します。
平均値が使える時は平均値や標準偏差による統計処理(パラメトリック)
ここからは、平均値が信頼できるデータにおける検定方法をご紹介していきます。先ほどの図で言うと右下に記載したものにあたります。平均値を中心に綺麗な山(正規分布)しており、平均値が集団の状態を反映したものである事が分かります。
このようなデータには以下のようなパラメトリック検定を行います。
パラメトリック検定で代表的なものがT検定であり、それを拡張し3群間比較を可能にしたものが分散分析(ANOVA)になります
T検定の流れについて説明する前に、普遍分散について軽くご説明いたします。普遍分散とは標本平均の分散を求める際に、分母をn-1にして求めたものになります。n-1にする理由については、また後日別の記事でご紹介いたします。今回重要なのはT検定を行う際には普遍分散を用いる必要があるという事です。
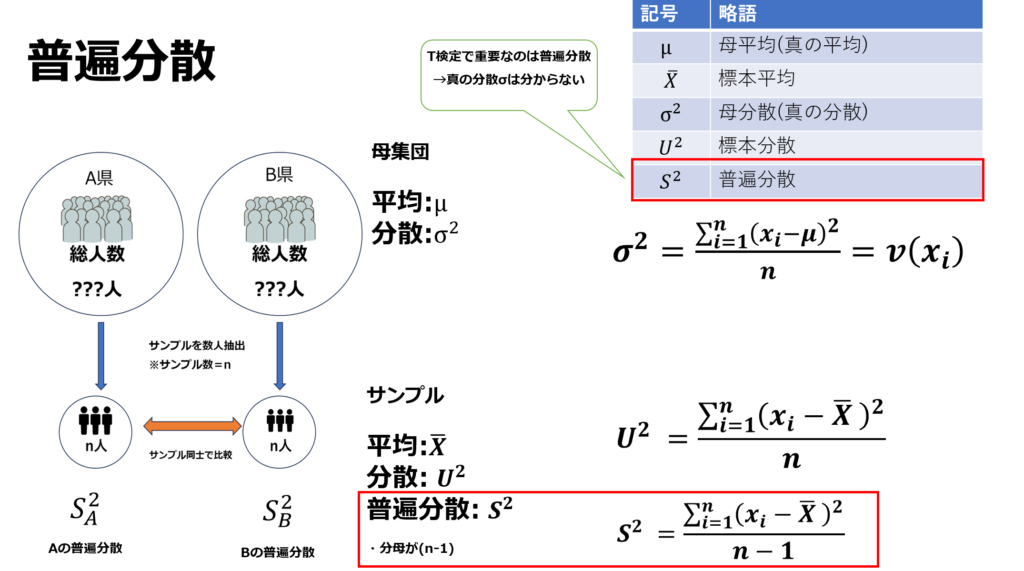
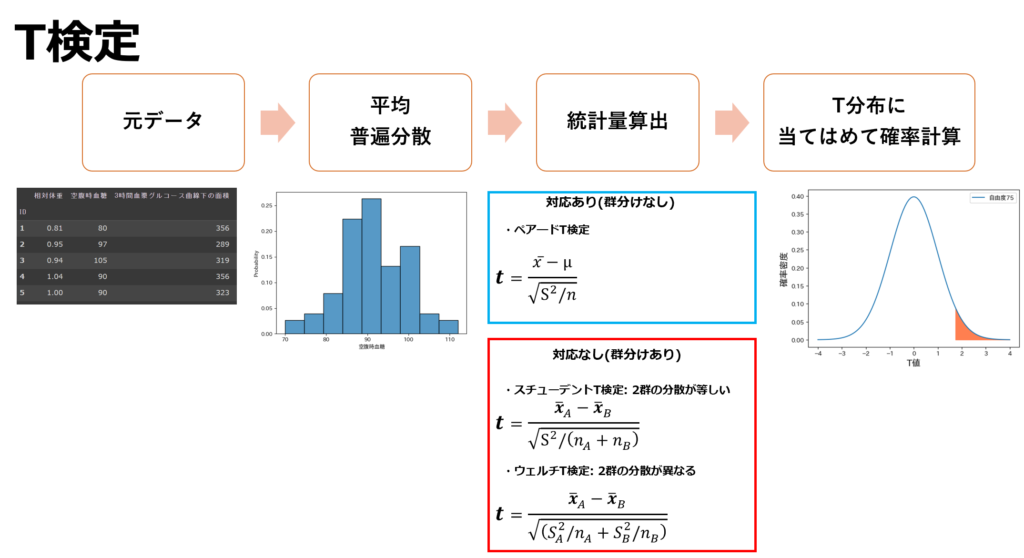
2群のT検定において、注意したいのは等分散性があるか否かによって統計量算出に用いる計算式が異なるという事です。2群の分散が大体等しい時はスチューデントのT検定(分母に郡全体の普遍分散を使用)、対して2群間で分散が大きく異なる時はウェルチのT検定(分母にA群、B群それぞれの普遍分散を使用)を行います。
対応のありなしについては後程説明しますが、簡単に説明すると比較対象が同一人物であるか否かです。
対応ありかなしか?
概要
対応のありなしを一言で説明すると、「比較対象が別人物であるか同一人物であるか?」です。
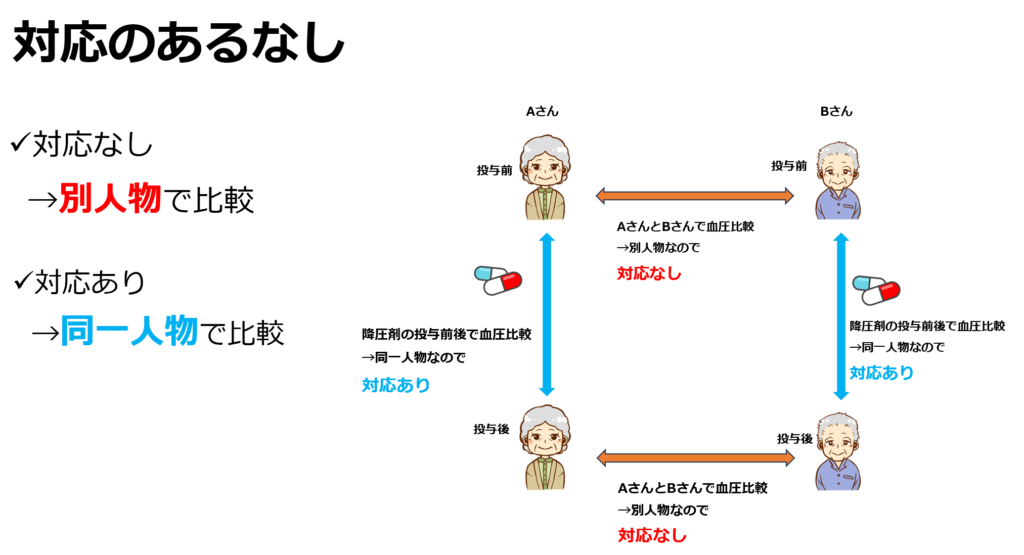
対応のある無しによって、使う検定が変わる事があります。T検定を例にして説明すると、対応あり検定では差を出してから平均値を比較、対して対応なし検定では平均値を出してからその差を比較します。

対応ありT検定と対応なしT検定の数式からも、対応ありでは変化量の平均値を、対応なしでは平均値の差を用いて検定統計量を算出していることが分かります。
対応ありは同一人物で比較し、その変化量を統合
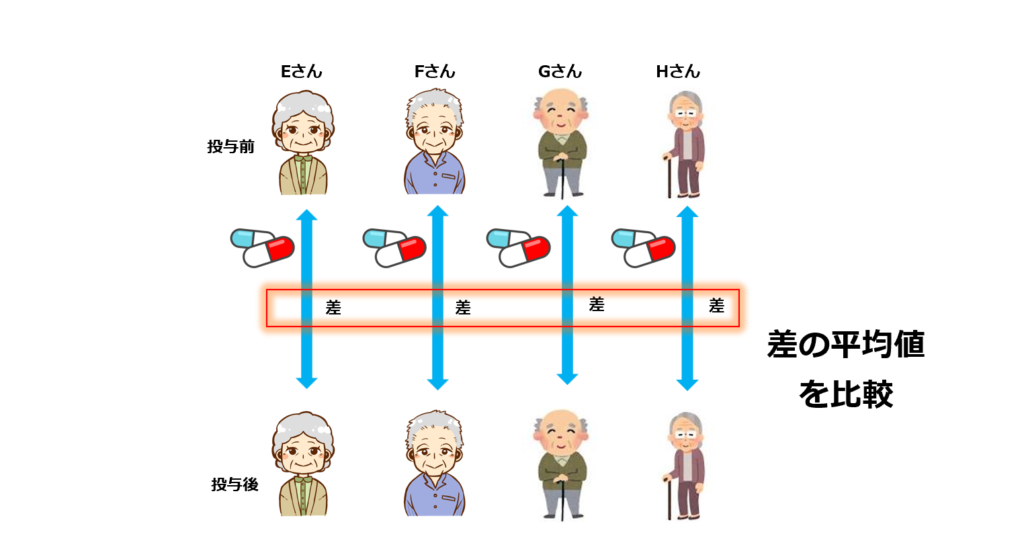
※ペア―ドのt検定
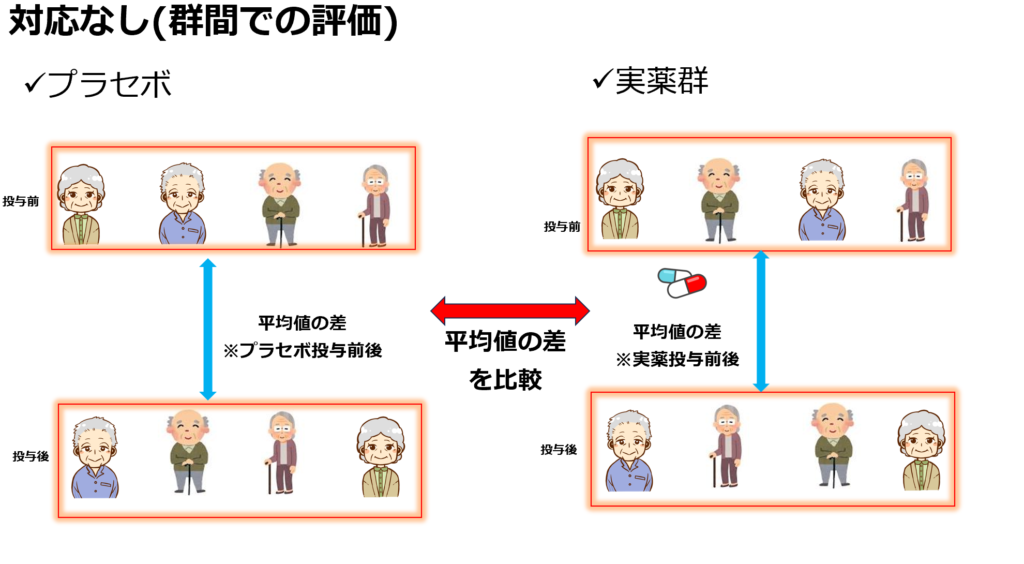
対応なしは群分けし、郡の平均値を比較
対応ありの場合、2群比較か3群以上の比較か?
対応なしの複数群間検定を行う場合。群の数が2群のみであるか3群以上で比較を行うか?も考える必要があります。2群の場合は、これまで説明したマンホイットニーのU検定やT検定での比較ができます。しかしこれらの検定で使用される式は3群以上に対応する事は出来ません。

※A群とB群の2群の順位及び群数から統計量算出

※A群とB群の2群の平均、普遍分散及び群数から統計量算出
ノンパラメトリックの3群間はクラスカルウォリス検定
まず、クラスカルウォリス検定になります。この検定は、マンホイットニーのU検定を3群間に拡張したものです。マンホイットニーのU検定同様にデータに対して順位付けを行いその順位を3群間で比較した有意差検定を実施します。
以下のデータはA、B、C組の身長の箱ひげ図になります。
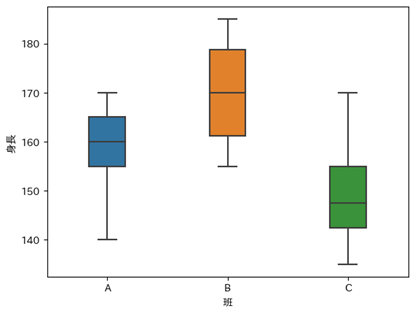
以下がクラスカルウォリス検定の流れになります。マンホイットニーのU検定と異なり、全ての群の順位和を統計量の算出に用いています。
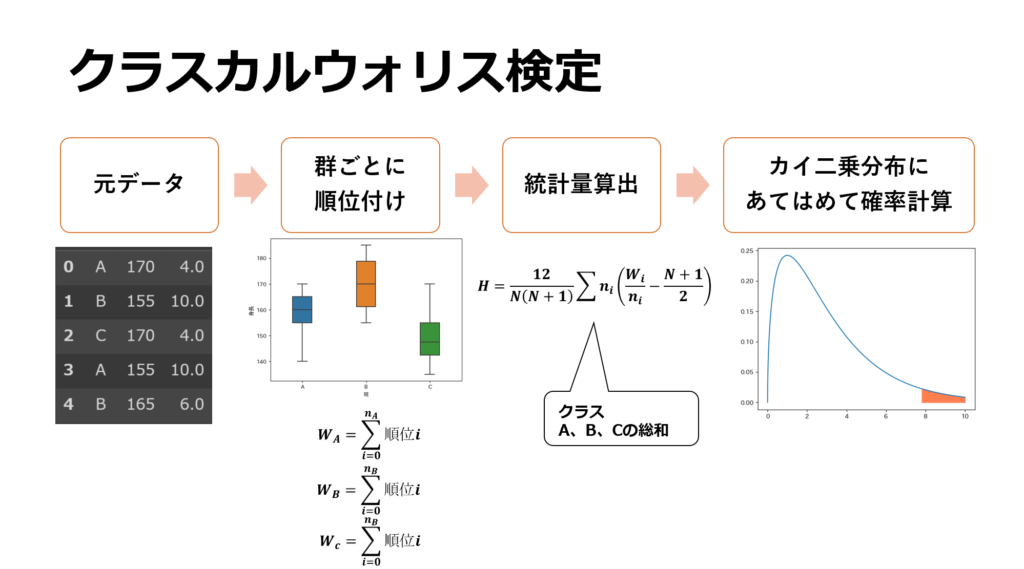
クラスカルウォリス検定では、各クラス毎の順位和を算出し、その値全てを用いて検定統計量を算出します。この検定統計量は、カイ二乗分布の確率密度関数に近似する事が出来るためこれを用いて有意差検定を行います。
クラスカルウォリス検定では、3群間のいずれかに有意差があるという事が分かります。
パラメトリックの3群間比較は分散分析
次に、分散分析になります。分散分析は郡内分散(グループ内での分散)と群間分散(グループ外での分散)を算出しそれぞれの大小関係から検定統計量を算出します。
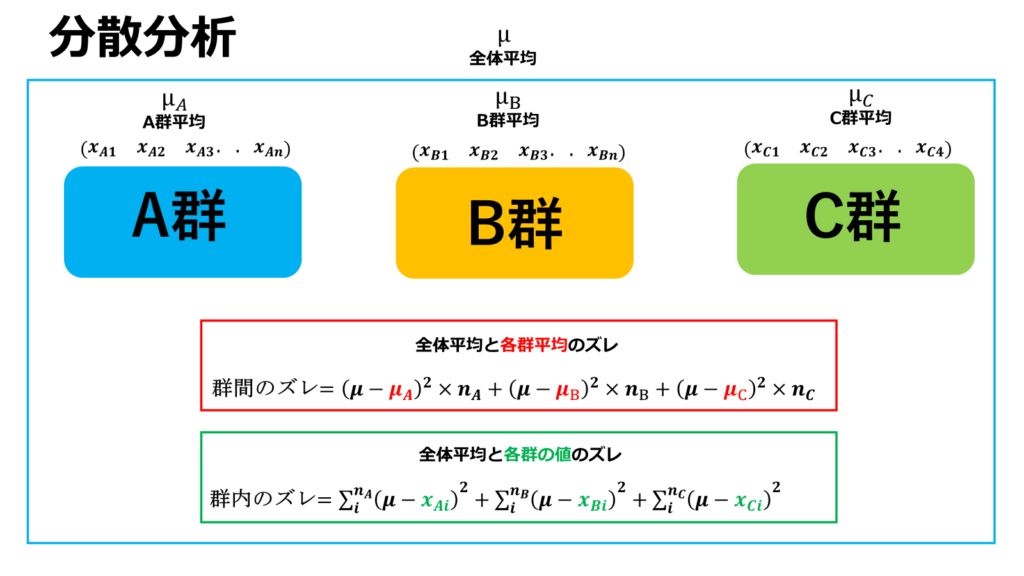
まず第一段階として全体平均を算出し、そこから各群平均とのズレの二乗和及び各群の値とのズレの二乗和をそれぞれ算出します。
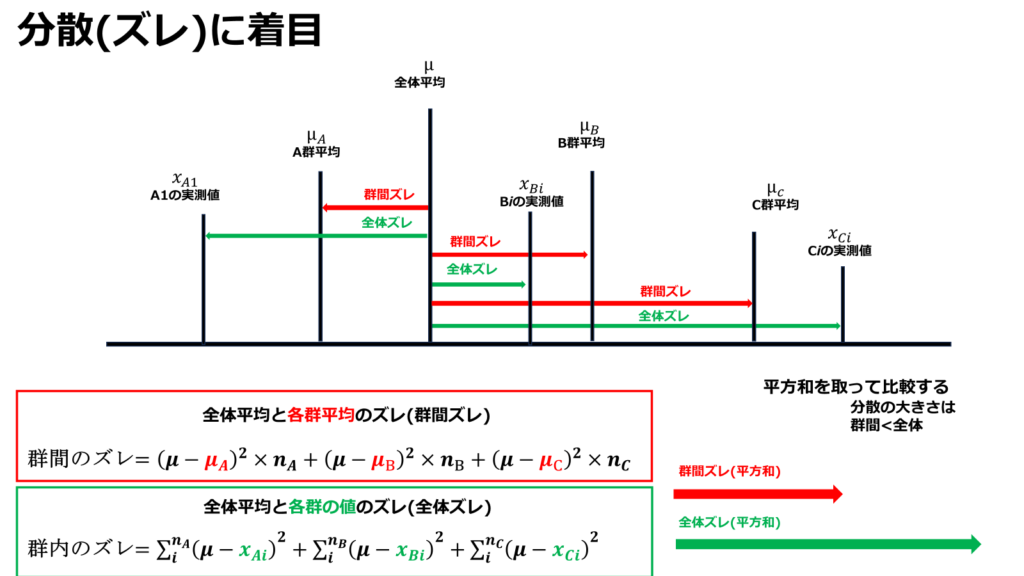

平方和とする理由は、差の算出だけでは負数になる可能性があるためです。
2乗する事で大小関係によるバラツキの大きさを評価する事が可能になります。
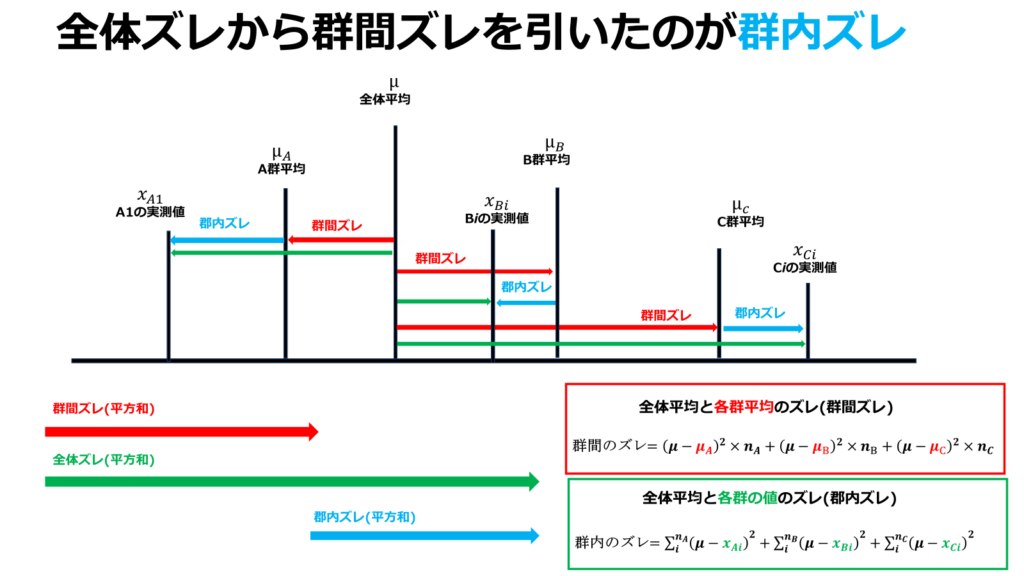
全体ズレの平方和から群間ズレの平方和を引くことで群内ズレの平方和を算出する事が出来ます。


群間ズレが大きいという事は、それぞれの群の値の差が大きい事を意味します。
対して郡内ズレは小さい方が群内でのデータのばらつきが少なく信頼性の高いデータであると解釈する事が出来ます。
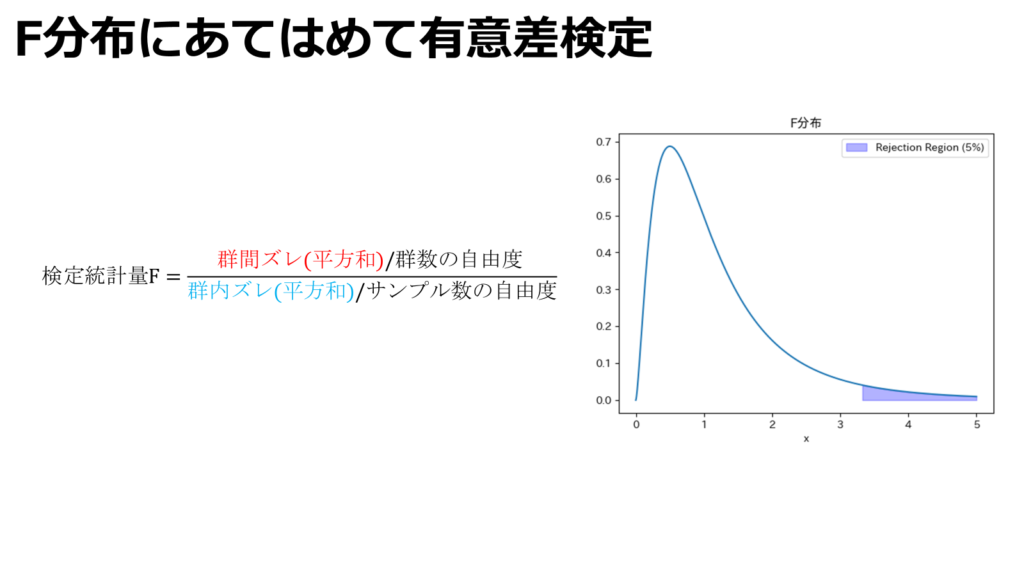
最後に群間ズレ平方和と郡内ズレ平方和及び、群数、サンプル数の自由度を用いて検定統計量を算出します。(自由度算出はT検定と同様)。この統計量がF分布に従うと仮定して有意差検定を実施します。
3群以上では事後検定も重要
ここで注意したいのが、3群間のどの組み合わせで差があるか?までは分かりません。このため、事後検定として多重比較を行う必要があります。これを行うことで、どこの群に差があるのかまで仮説検定をすることが可能になります。
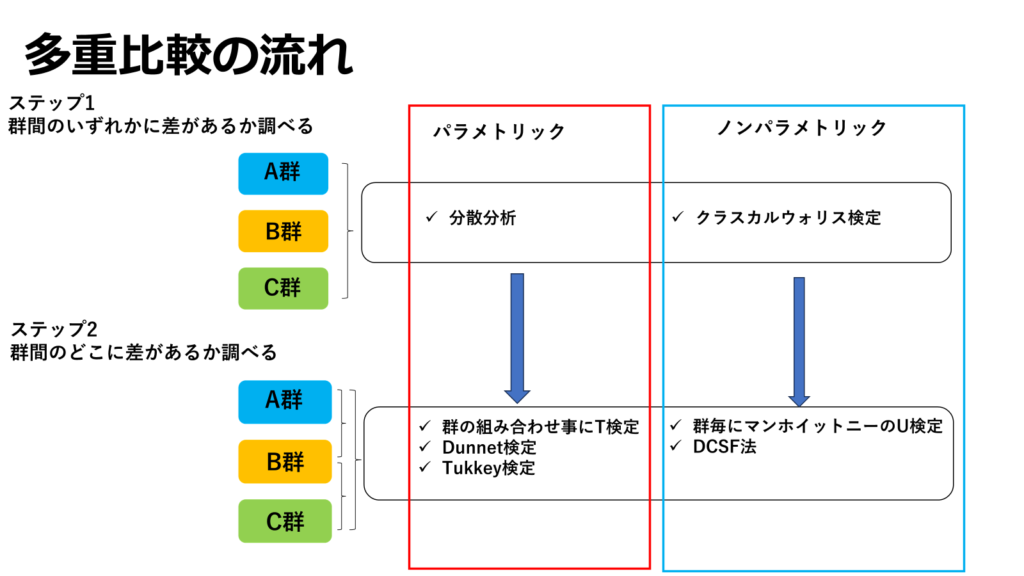
第一段階では分散分析や、クラスカルウォリス検定を用いて3群間のいずれかに差があるか?を確認します。ここで差が認められれば、事後検定として多重比較を行います。多重比較
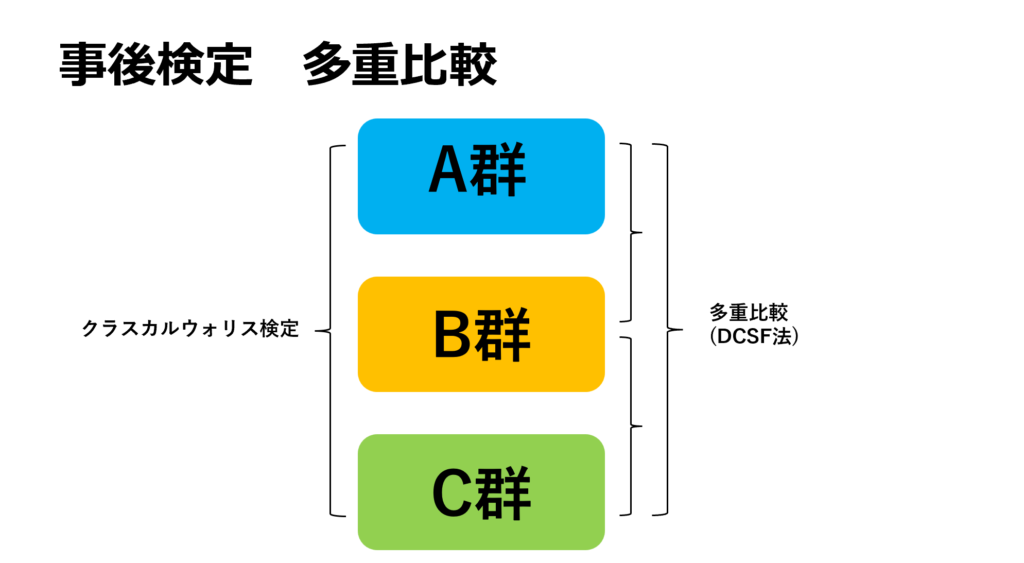
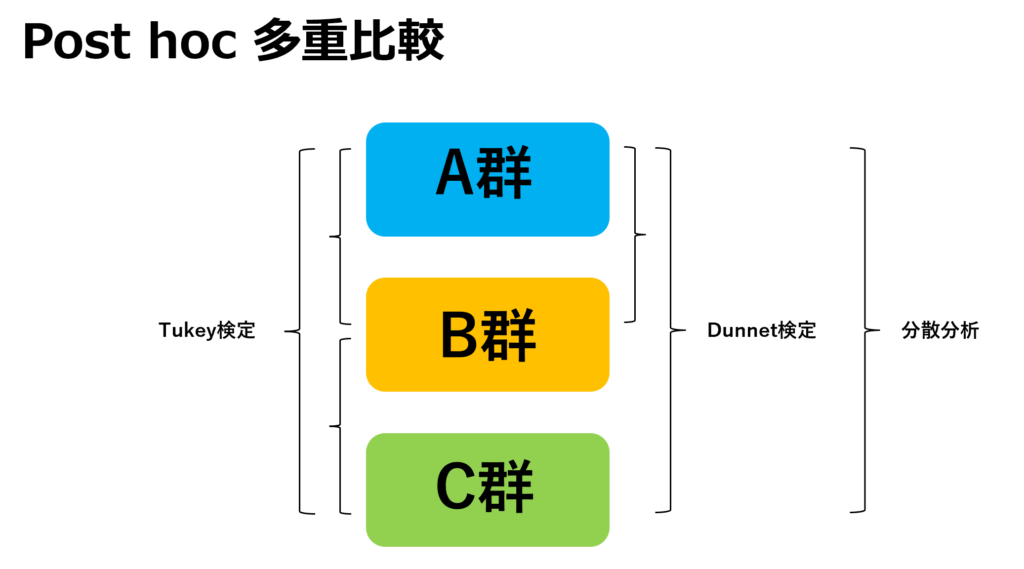
実際、この流れについて過去の薬剤師国家試験で出題された事もあります。全体の検定を行ってから事後検定を行う事、パラメトリックかノンパラメトリックかによって用いる検定が変わる事等が分かっていれば正答可能です。
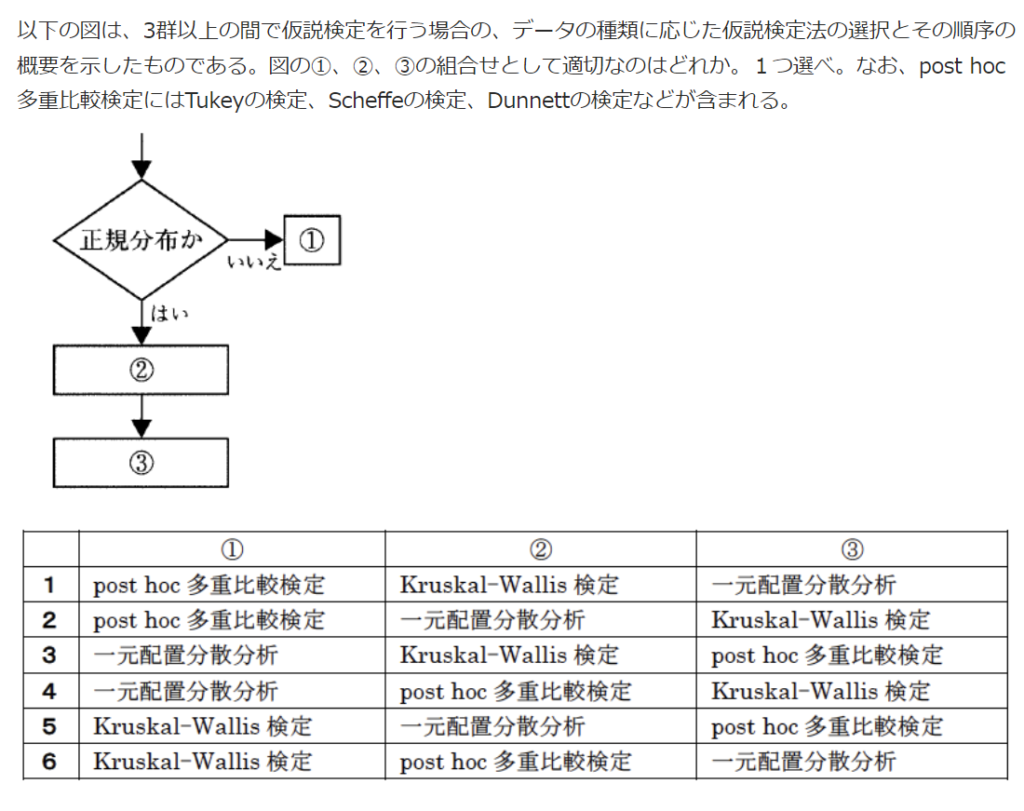
「検定」に焦点を当てるか「推定」に焦点を当てるか(両方やることもあります)
差が有るか無いか?(Yes or No)をはっきりさせたい時は仮説検定を、母集団でどの程度差があるか?を知りたい時は区間推定を、目的変数に対して説明変数がどの様な影響を及ぼすのか知りたい場合は回帰分析を行います。
| 手法 | 目的 |
|---|---|
| 仮説検定 Ex)カイ二乗検定、マンホイットニーのU検定、T検定 | ・母集団に於いて差が在るかないか?を推定する Yes or No 事例) 薬剤A群と薬剤B群では薬剤B群の方が平均血圧が5mmHg低かった 母集団に於いても本当に5mmHg低いの? →仮説検定を行う ※p値=母集団で差が認められない確率 p = 0.05であれば5%の確率で母集団では差が認められない可能性がある |
| 区間推定 Ex) ・正規分布もしくはT分布を用いた95%信頼区間の算出、 ・二項分布 ・オッズ比、相対危険度の信頼区間 | ・母集団に於いてどの程度差が在るか?を推定する 事例) →薬剤A群と薬剤B群では薬剤B群の方が平均血圧が5mmHg低かった 母集団ではどれくらいの差が認められるの? →区間推定を行う ※95%CL(3.51mmHg~4.5mmHg) 母集団におけるAとBの平均の差は、95%の確率で3.5~4.5である。 |
| 回帰分析 Ex) ・重回帰分析 ・ロジスティクス回帰分析 | ・説明変数から、母集団における説明変数を予測する。 ・説明変数に対する目的変数の影響度を推測する。 事例) ・身長○○、体重××、年齢△△歳の場合母集団における腎機能はどれくらい?(説明変数予測) →それぞれの重みから影響度を推測する事も出来る。 ※後日別の記事で詳しく説明します。 |








コメント