限られたデータから予測を立てられちゃう!
医療統計学の基礎を学ぶ:基礎知識と次の記事への準備
突然失礼いたします。本記事では、医療統計学の基礎について解説します。医療統計は、データ解析や検定の選択において重要な役割を果たします。この記事では、統計学の基礎に焦点を当て、次の記事では具体的な検定方法や計算手順について詳しく説明していきます。
本記事の続編として、こちらをお読みいただければと思います。
対象読者
- 医療統計学を大学で学ぶ事になる薬学部生。
- 研究や実務実習などで論文を読む機会がある薬学部4~6年生。
- 数学が苦手な薬学生、薬学部入学予定の高校生
- 統計をしっかり理解したい薬学生
統計の目的
はじめに
薬学部で学ぶ科目の一つに、「医療統計学」があります。論文や文献調査を行う際、必ず目にするのが図表や統計データです。これらに記載された数値の信頼性をどの程度評価できるのか、またその結果をどのように解釈すべきかを理解することが、医療統計学の学習目的となります。
107回薬剤師国家試験 304 305 厚生労働省ホームページ
「母集団」と「標本」という概念
まず初めに、医療統計学の基礎となる「母集団」の概念を理解することが重要です。例えば、都道府県Aと都道府県Bの住民の平均血圧を比較したい場合を考えます。アンケートや調査を実施することになりますが、全ての県民の血圧を漏れなく正確に調査することは、現実的には不可能です。
ここで役に立つのが統計学(母集団と標本)です。
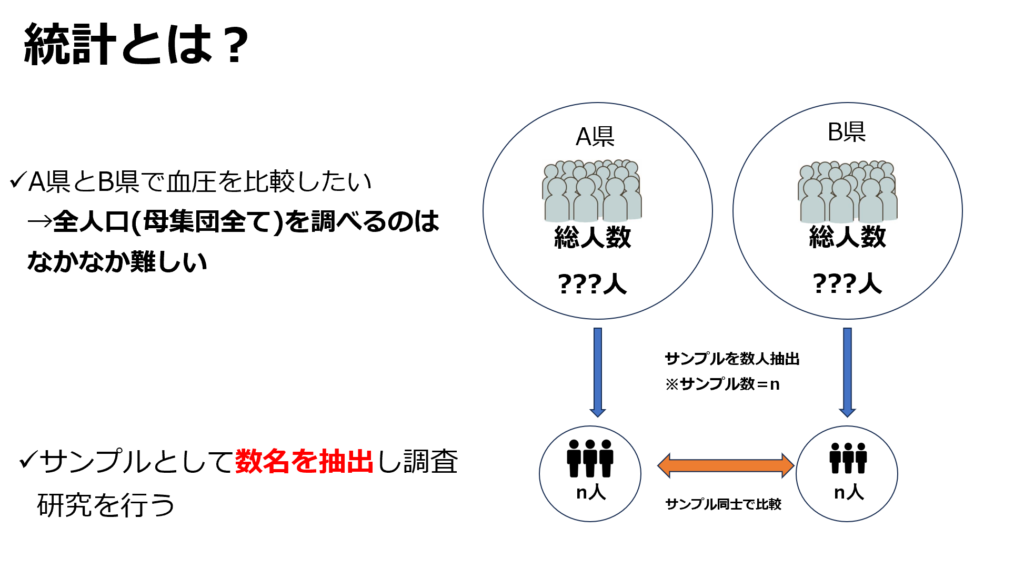
都道府県Aと都道府県Bの住民の血圧を比較するためには、全ての県民を調査するのではなく、各県からサンプルとして数名の対象者を抽出します。この抽出は、統計的な正確性を保つために無作為抽出で行われます。
具体的には、調査の結果に偏りが出ないよう、特定の条件(例えば身体能力の高い人)を基準に選抜してはいけません。無作為に選ばれた対象者によって、より信頼性のある結果が得られます。
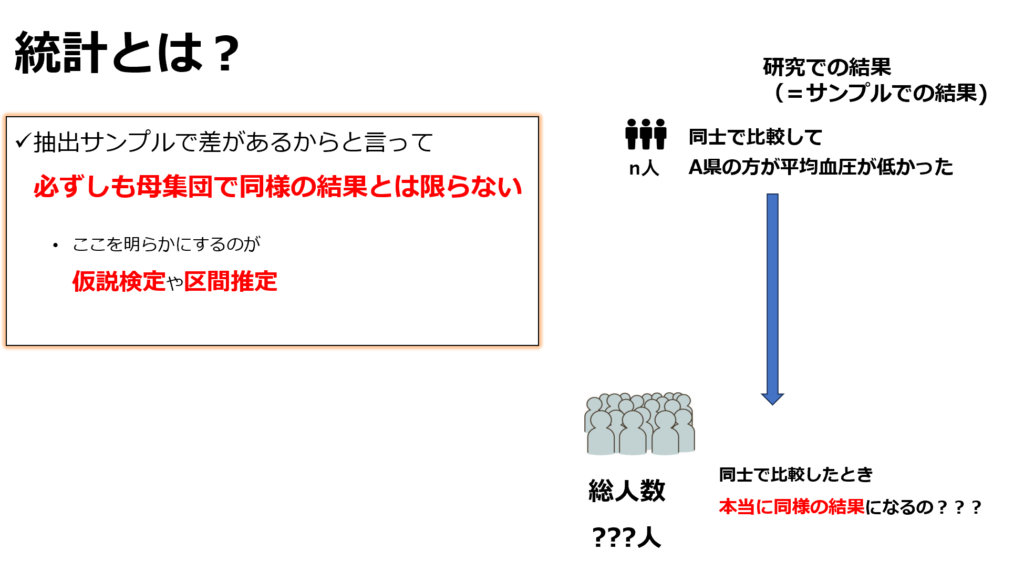
仮に、サンプルを比較した結果、A県とB県の住民の平均血圧に差が認められたとします。
しかし、この結果が本当に母集団全体にも当てはまると言えるでしょうか?この疑問を解決するために、確率論に基づく考え方が必要です。統計学は、サンプルの結果を基に母集団全体で同様の傾向が見られるかどうかを判断するための強力なツールを提供します。
サンプルから得られたデータを統計的に処理することで以下の事が分かります
- サンプルで出た結果が、母集団でも同様の結果である確率(仮説検定)
- サンプルで出た結果が、母集団ではどの程度の範囲でズレているか?(区間推定)
- サンプルの結果から母集団における値を推定する(回帰分析)
中でも、仮説検定が非常に重要になります。というのも、実際の分析では、区間推定や回帰分析を行った際にその結果の精度、信頼性評価として仮説検定を行う事があるからです。
仮説検定を行う上で重要になるのは、帰無仮説と対立仮設、過誤、p値と有意水準等の考え方になります。
仮説検定について
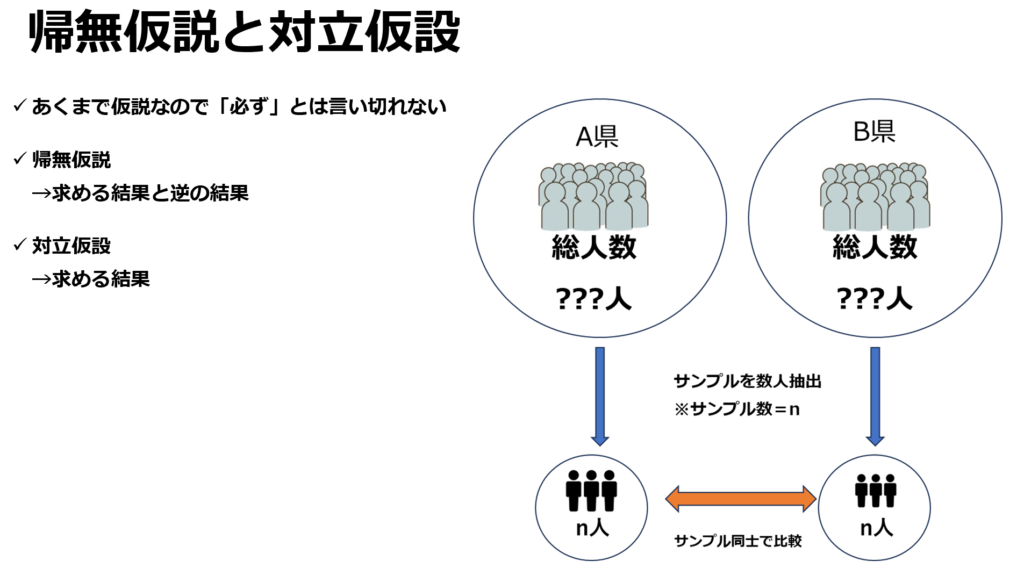
帰無仮説と対立仮設
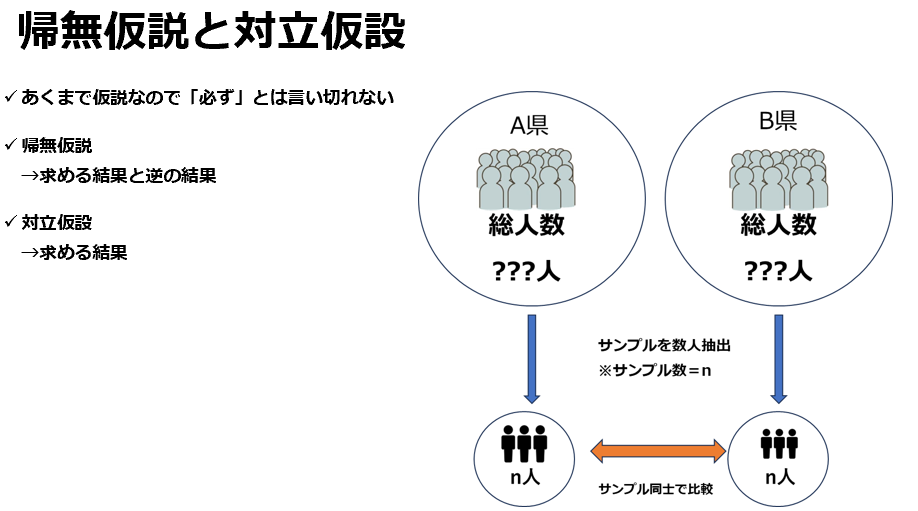
対立仮説とは研究で求める結果であり、対して帰無仮説とは研究で求める結果とは逆の結果になります。
ここで注意したい点が二つ程あります。1つ目は、研究目的によって帰無仮説と対立仮設は変わる事、2つ目はあくまでも「仮説」であるため絶対はあり得ないという事です。
統計解析の結果、対立仮設が採択されたとしても、対立仮設が「肯定」されたわけではなく、帰無仮説が「否定」される訳ではありません。
帰無仮説も同様で、こちらが採択された場合でも帰無仮説が「肯定」される訳ではなく、対立仮設が「否定」される訳ではありません。
こう考える理由は、統計学的処理が確率論に基づいた処理であることに起因します。後述するαエラー(第1種の過誤)とβエラー(第2種の過誤を)起こしうる確率を計算するのが仮説検定における統計処理になります。
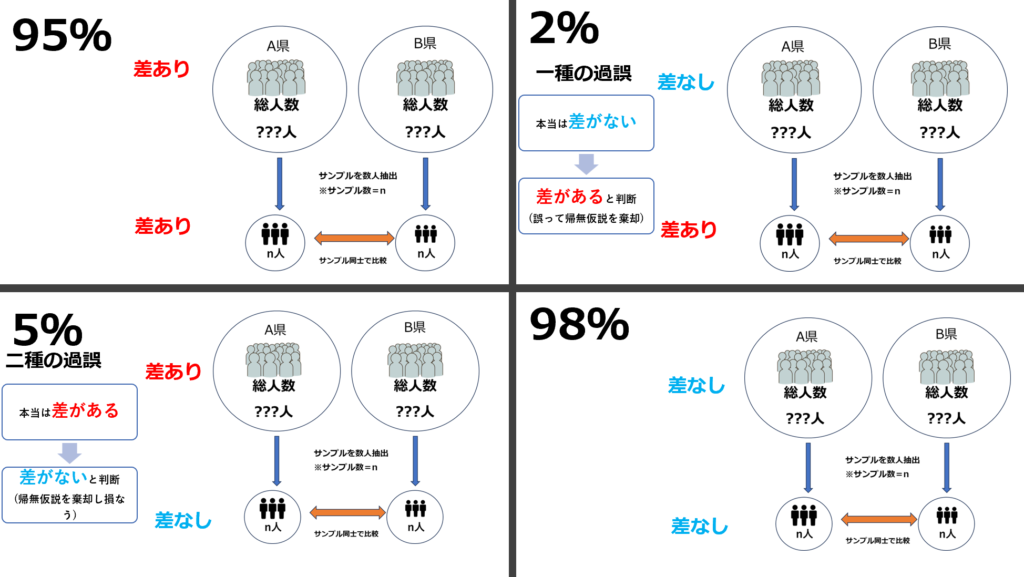
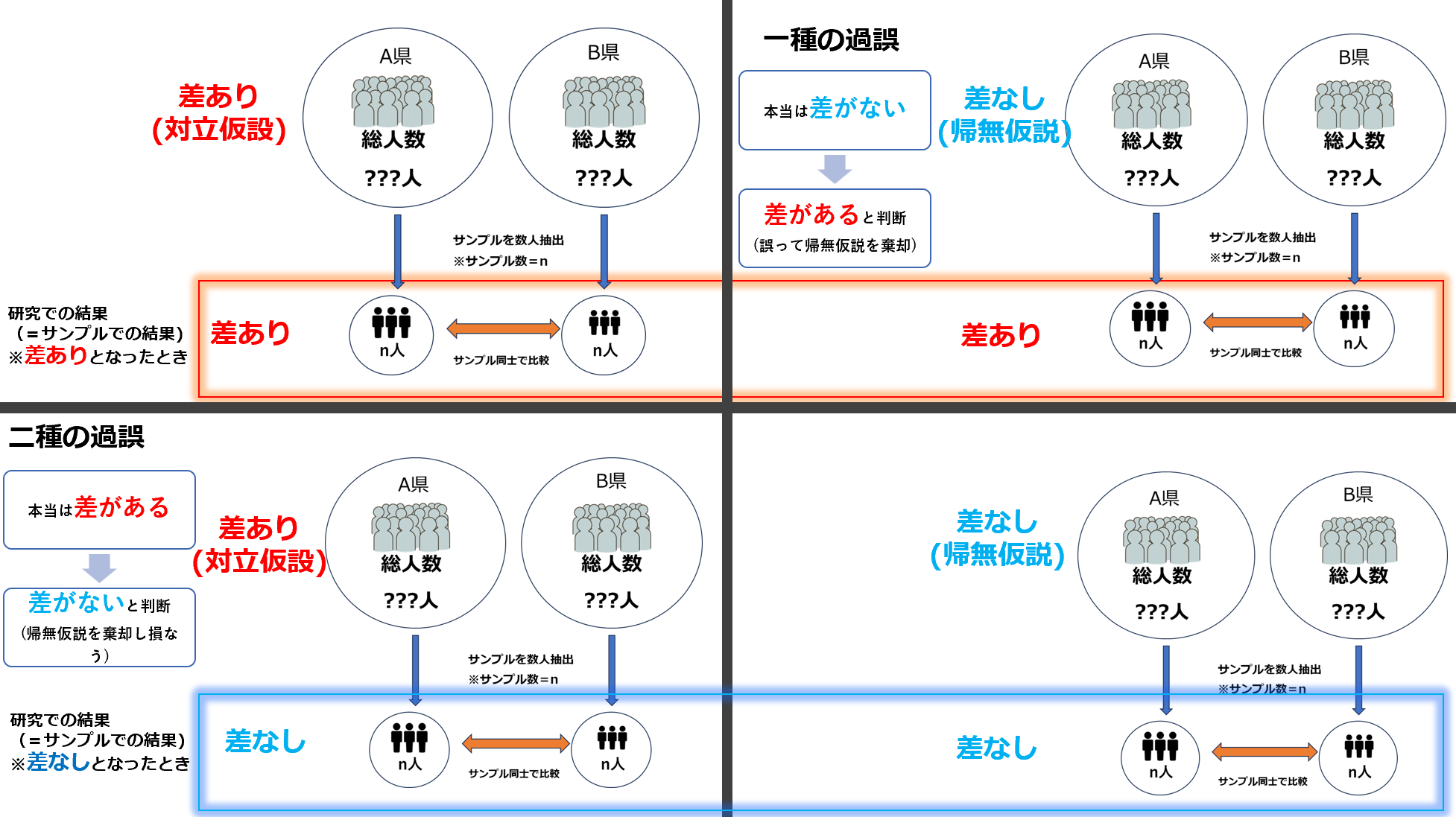
第一種の過誤(αエラー)と第二種の過誤(βエラー) 重要!
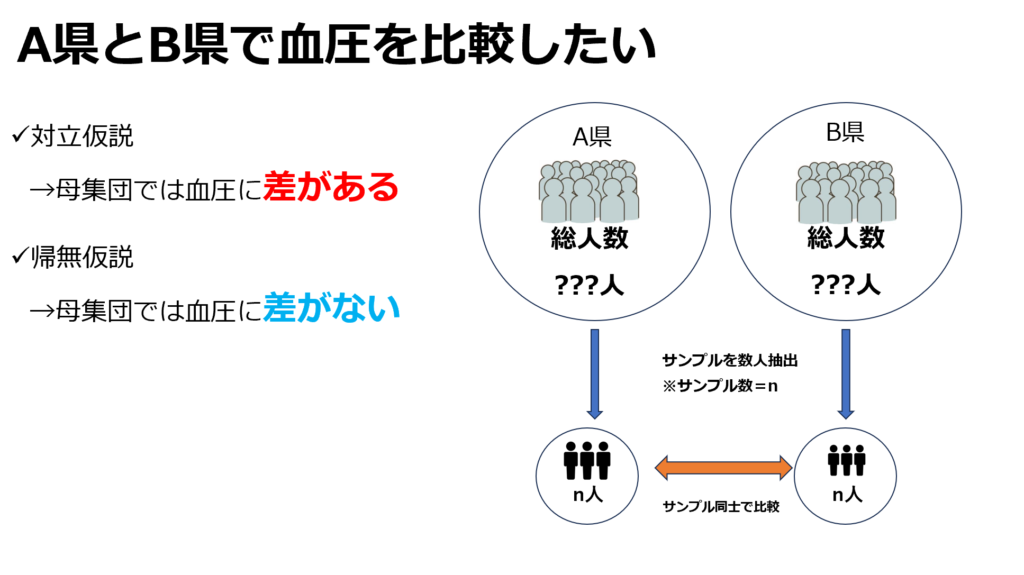
対立仮設を、「A県とB県で平均血圧に差がある」とし、帰無仮説を「A県とB県で平均血圧に差が見られない」とします。サンプルと母集団では以下の4つの組み合わせが考えられます
- サンプルでも母集団でも同様に差がある
- サンプルでは差があるが、母集団では差がない
- サンプルでは差がないが、母集団では差がある
- サンプルでも母集団でも差が見られない
上記のうち赤太字で記した2行は研究結果と母集団(真の結果)が矛盾していることになります。このことを統計学的に「過誤」と呼びます。
過誤は、大きく分けて「第一種の過誤」と「第二種の過誤」に分類されます。
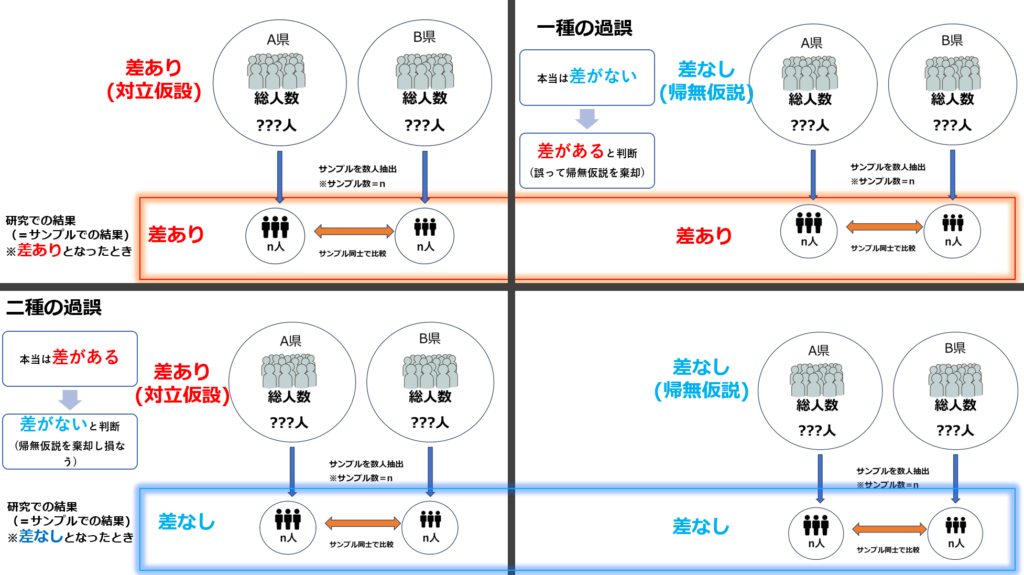
- サンプルでは差があるが(対立仮設)、母集団では差がない(帰無仮説)
→第一種の過誤
※誤って帰無仮説を棄却してしまっている。 - サンプルでは差がないが(帰無仮説)、母集団では差がある(対立仮設)
→第二種の過誤
※棄却しなければいけない帰無仮説を棄却できていない。
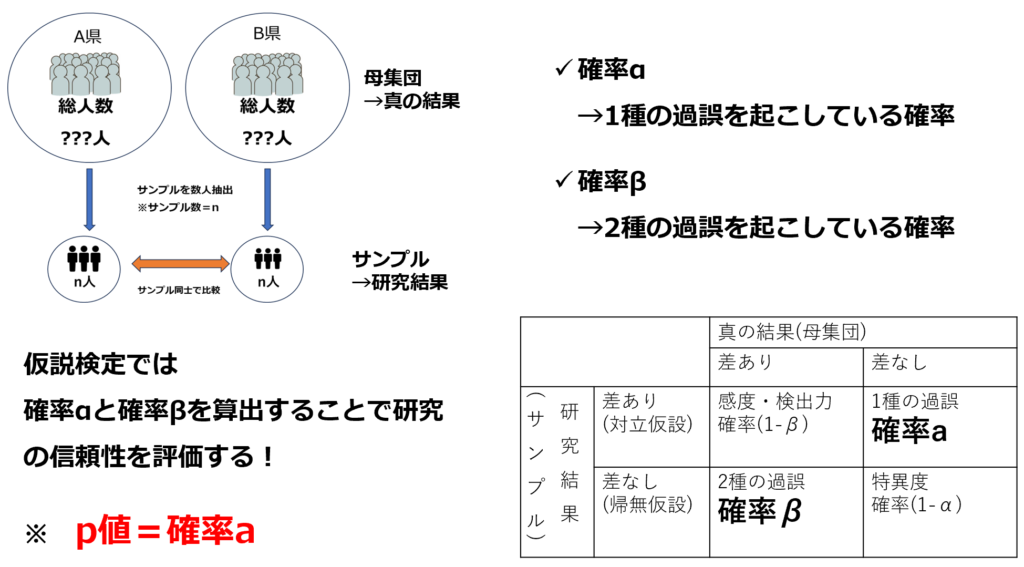
統計学で取り扱う○○検定では、平均値、分散、順位などの数値から確率αを算出することが出来ます。そしてこの確率を算出するために数学的な考え方を用いる事になります。]
Ex) T検定、マンホイットニーのU検定、カイ二乗検定、ログランク検定など。
p値と有意水準について。
p値とは、αエラーを起こしている確率になります。分析対象データを統計ソフトに入力するとこの確率を自動的に算出し出力してくれます。
統計ソフトでは、検定を行うと以下のように出力されます。pythonのstatモジュールを利用しました。元データはランダムで作成したものになります。
#T検定を行った場合(pythonのstat t-testモジュール)
>>>TtestResult(
statistic=-0.806212183720361,
pvalue=0.21041959484883888,
df=266.5560992261538)p値が約0.2と出力されていることから、第一種の過誤を起こしている確率は約20%であると解釈することが出来ます。
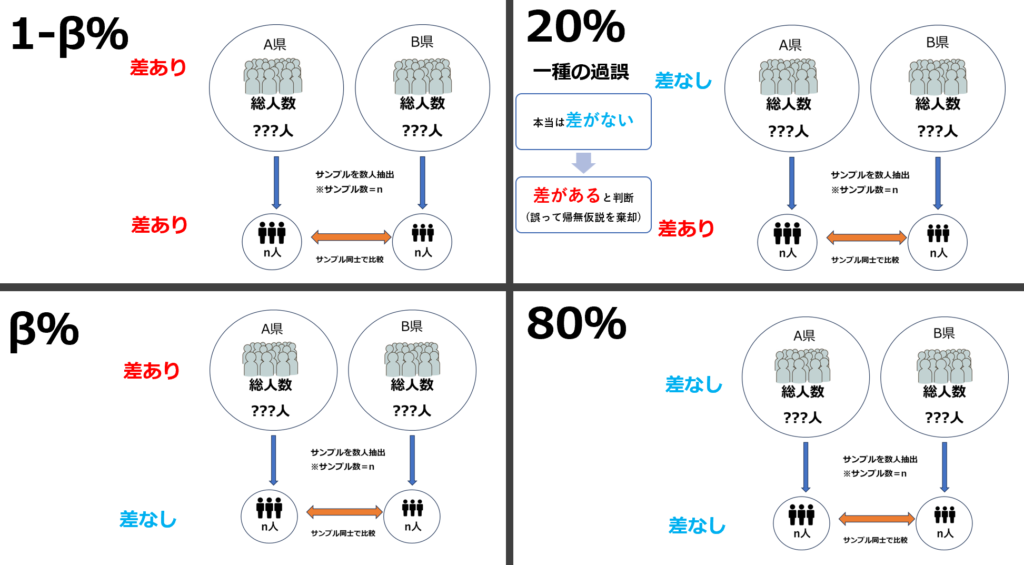
また、後述しますが検定を行う際は「有意水準」という指標に基づいて仮説検定の結果を評価します。そして、「有意水準」とは、第一種の過誤をどこまで許容するか?の基準になります。
試しに統計データを解釈してみよう(仮説検定)
過誤の割合から真実を確率予測!
以下のような研究結果が得られたとします。

サンプル抽出の結果血圧に差が認められましたが、それは本当に県全体でも同様の結果であると言えるのでしょうか?
α値(第一種の過誤率,表中ではp値として記載)が2%程である事、β値(第二種の過誤率)が5%程である事より以下のように解釈します。
有意水準に基づいた帰無仮説の棄却(重要)
「有意水準」とは、第一種の過誤をどこまで許容するか?の基準になります。
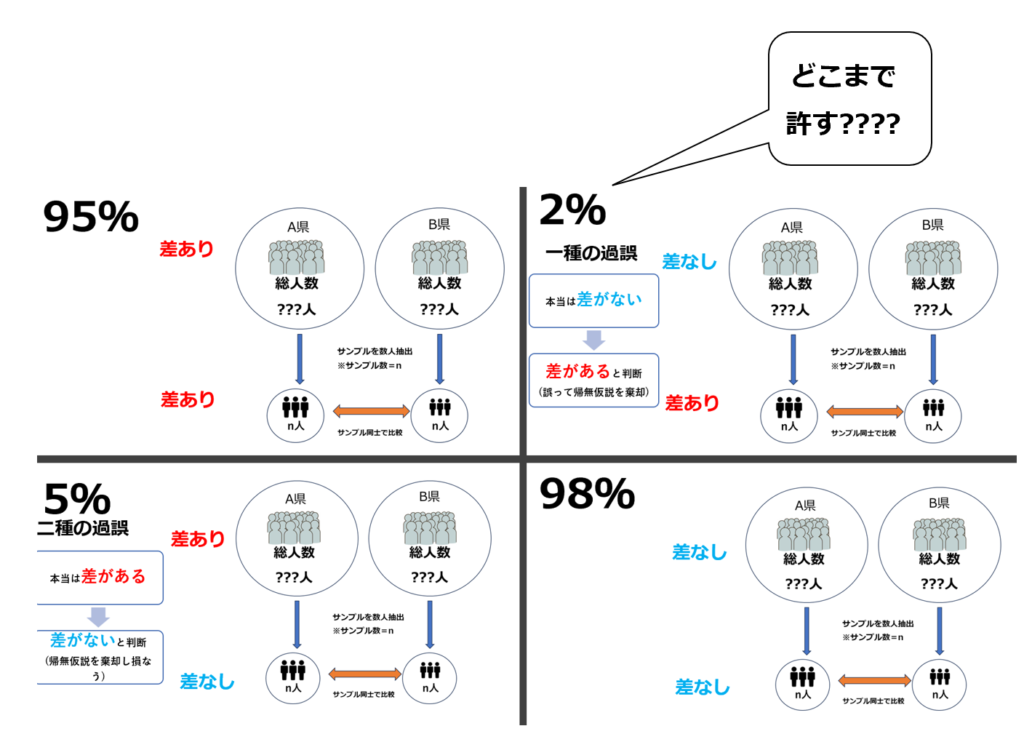
そして、その基準をクリアした場合帰無仮説は棄却されたこととなり、「有意差が認められた」と表現する事が許されます。※対立仮設の採択

仮設なので対立仮設が「肯定される」訳ではありません!
※国家試験頻出引っ掛けパターン

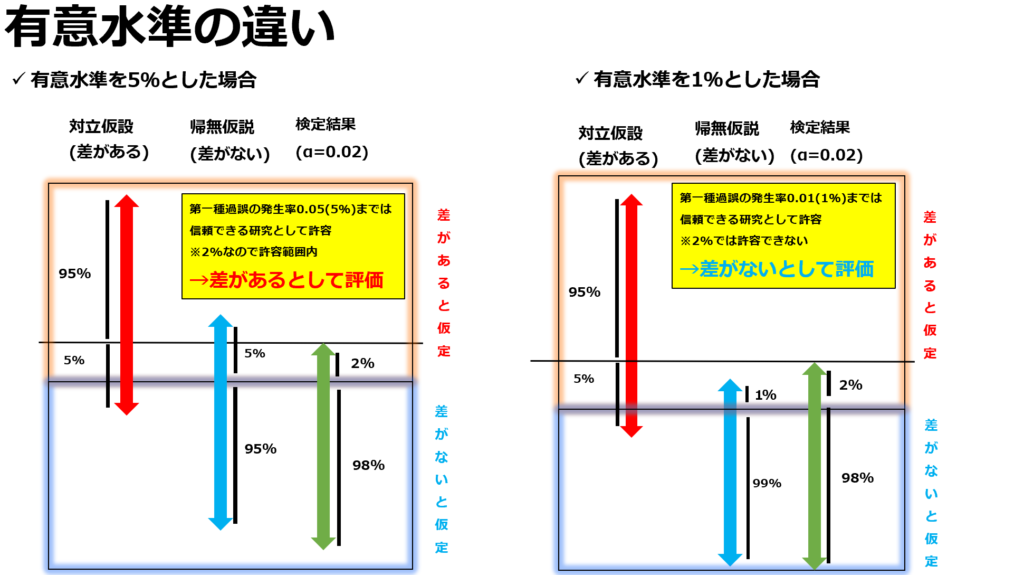
上記の研究ではp値が0.02です。このため有意水準5%で検定を行った場合、帰無仮説を棄却し対立仮設を採択する事が出来ます。
しかし有意水準1%で研究を行った場合はこの基準値を上回ってしまっているため帰無仮説を棄却出来ません。

上記の場合、有意水準5%では「有意差あり」として合格になりますが、有意水準1%にした場合は「有意差は認められない」として不合格になります。

水色で記した分布は帰無仮説の分布(検定手法ごとに決められているもの)、赤色で記したグラフは対立仮設(サンプルから推定したに分布)になります。
p値を算出する際は、帰無仮説の分布に基づいて第一種の過誤率が算出されます。このためp値が低くなるとそれに応じて検出力(1-β)も向上していきます。また、サンプル数が増えていくとそれに応じて分布も狭くなるためp値の低下及び検出力の向上が期待できます。
https://bellcurve.jp/statistics/course/12767.html
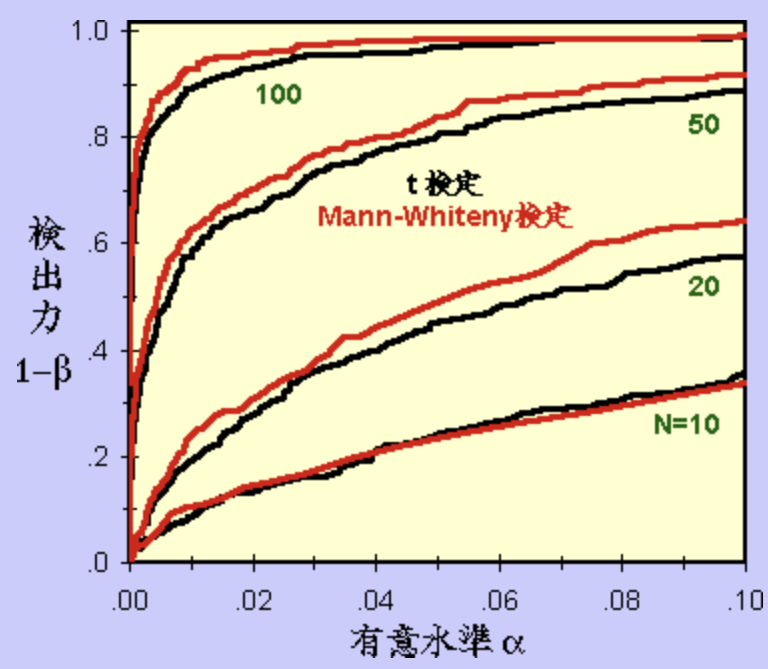
以下の記事で、t検定とマンホイットニーのU検定における有意水準(αエラー率)毎の検出力(1-β)の変化を可視化されている方がいましたのでご紹介させていただきます。
https://syodokukai.exblog.jp/iv/detail/?s=21161527&i=201409%2F29%2F74%2Fd0194774_22303090.jpg
まず右図のような2つの正規集団を用いて、t検定 と Mann-Whiteny検定 の検出力を比較してみましょう。2つの集団からランダムにN個づつ抽出して、検定する過程を300回繰り返しました。 https://www.angelfire.com/dc/coulmbo/Stat/Easy/power_U.html
統計で学ぶべき事
データの特徴と種類
まず最初に、データの種類について正しく理解する必要があります。大きく分けてカテゴリカルデータと量的データに分類されます。この二つの違いを一言で説明すると、カテゴリデータは連続していない数値、量的データは連続している数値になります。
カテゴリデータ(定性的データ)
名義尺度
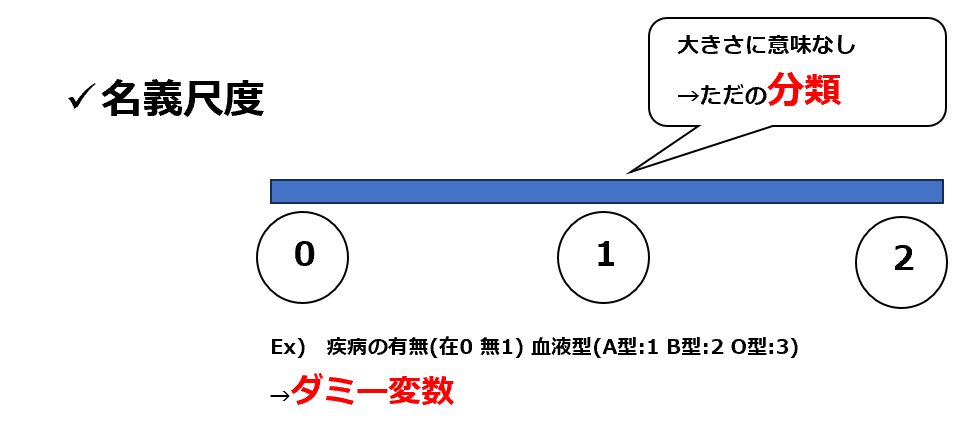
カテゴリデータはその数値の大きさに意味を持たない「名義尺度」と大きさに意味を持つ「順序尺度」に分けられます。
名義尺度の例として性別や学籍番号があります。男性-女性という言葉では統計処理をすることが出来ません。このため男性であれば1を割り振る、女性であれば0を割り振ると言った処理を施す事で統計処理を可能にしています。
学籍番号も同様で、学生ごとに番号を割り振る事で学生の判別を可能にしています。名義尺度の特徴として数字の大きさに意味を持たないということが挙げられます。学籍番号は、学生の判別目的で割り振られているものであり、この数字が大きいからと言って優れている(もしくは劣っている)訳ではありません。
順序尺度
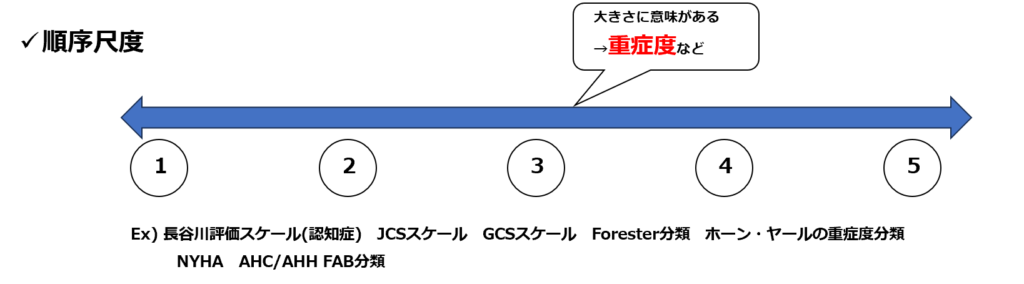
順序尺度の例としては重症度分類などが該当します。こちらは、数字の大きさに意味を持ちます(重症度によって値が上下する)。
カテゴリデータの注意点

カテゴリデータの注意点として、平均値で評価をする際は注意が必要です。名義尺度に至っては平均値が使えない事もあります。例えば男性を1、女性を0として割り振ったとします。この平均が0.6だったとしましょう・・・・

性別どっちだよ!!!
ってなりますよね・・・・
順序データも同様で、例えば5段階のランク分けがされているもので、平均ランクが3.2です。と言われてもそれは正確な値を出せているとは言えません・・・
これらのデータを統計処理する際は、順位で比較する(マンホイットニーのU検定)、存在割合で比較する(カイ二乗検定、Fisher検定)など平均値や分散に依存しない統計処理を利用する必要があります。
※T検定は平均値、不変分散を用いて統計量を算出する検定手法であるのでカテゴリデータには向いていません。
量的データ
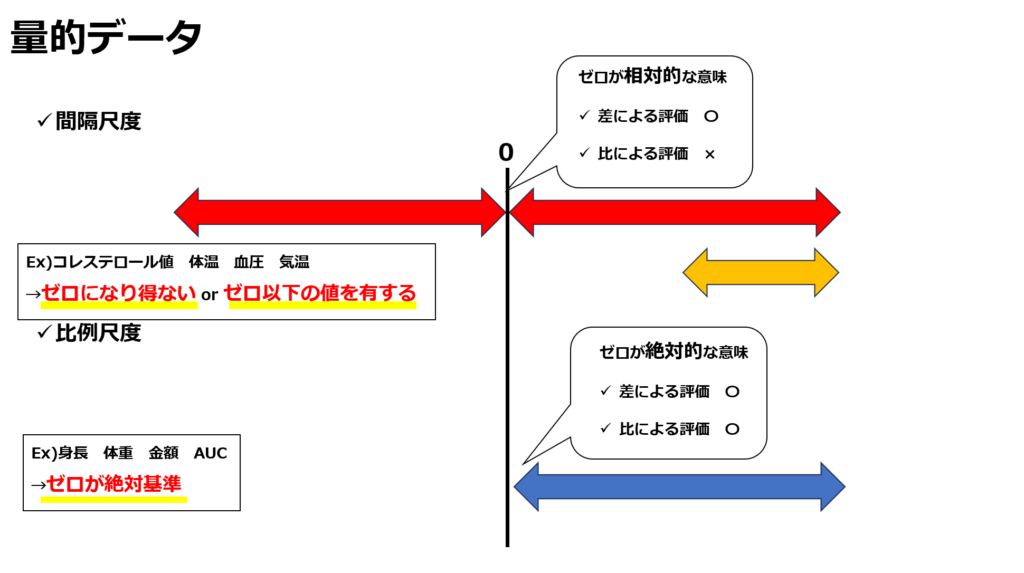
数値データは数値が連続的な値であり、その大きさにも意味を持つものです。中でも絶対的な基準値が決められている数値の事を比例尺度、基準がなく相対的に評価するものを間隔尺度と呼びます。これらの検定はカテゴリデータとは異なり平均値を算出して評価する事が可能です。このため場合によってはT検定を行う事も可能です。
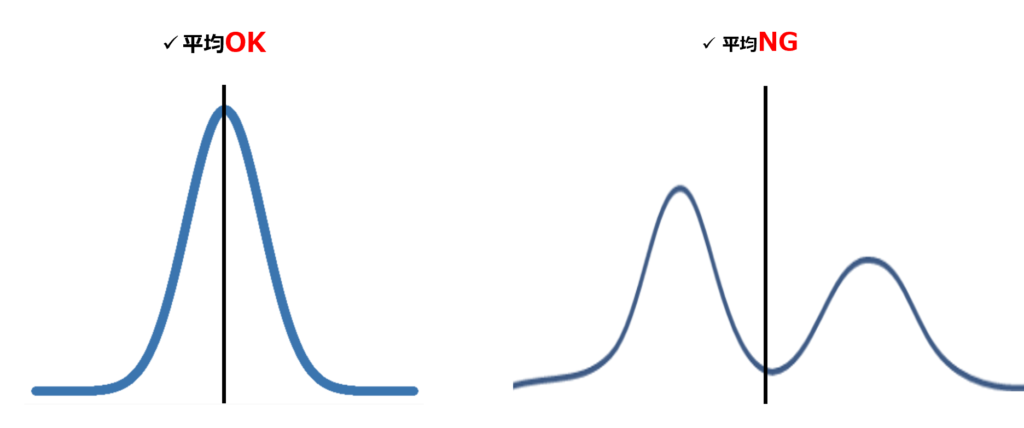
ただ、正規分布をしていないデータの場合は平均値の使用は注意が必要です。というのもデータがばらばらの場合は、平均値が必ずしも集団の状態を反映しているとは言えないためになります
検定手法の選択
検定手法を正しく選択する事の重要性について説明いたします。まずは下記の表をご覧ください。
- 元データ(ダミーのデータですので本物の結果ではありません)
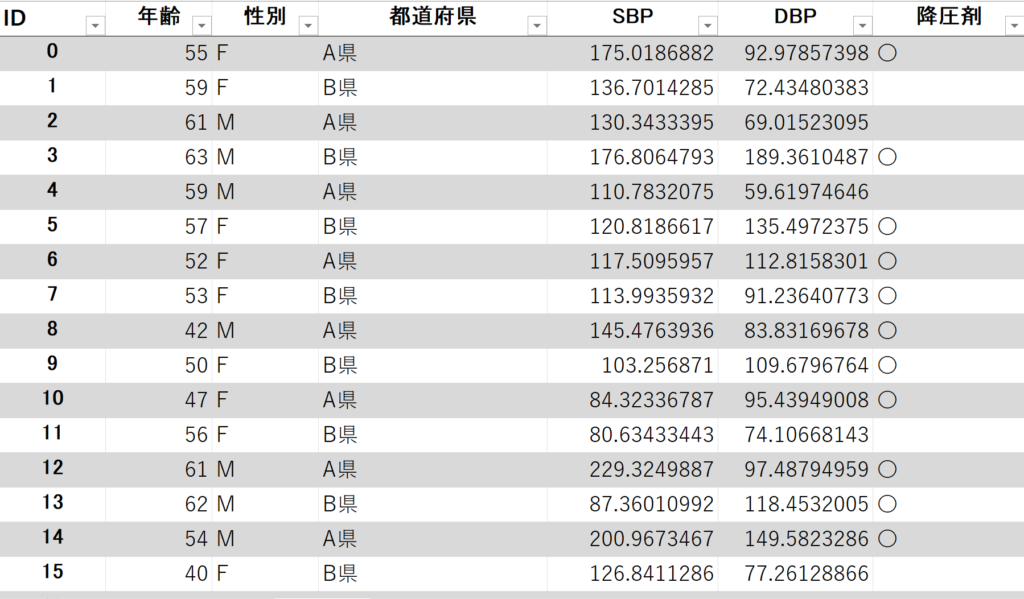
上記のデータにT検定とマンホイットニーのU検定をそれぞれ行いました。
#県ごとの平均血圧(±標準偏差)
>>>
A県:平均血圧137(±30.6)
B県:平均血圧140(±30.3)#T検定を行った場合
(pythonのstat t-testモジュール)
>>>TtestResult(
statistic=-0.806212183720361,
pvalue=0.21041959484883888,
df=266.5560992261538)#マンホイットニーのU検定を行った場合
(pythonのstat t-testモジュール)
>>>MannwhitneyuResult(
statistic=11590.0,
pvalue=0.22985238993550006) 結果を比べてみると、前者のp値が約0.21であるのに対して後者では約0.23とズレが生じています。これは仮説検定を行う際、元データの性質によって検定手法に向き不向きがある事に起因します。
※前述した平均値の信頼性などが影響

これには、前述した平均値の信頼性等が関与しています。
データごとにどの様な検定を使うべきか?そもそも何故このようなズレが生じてしまうのか?などを知っておかなければ、誤った解釈をしてしまうことに繋がりません。このためデータの性質を知り、正しい検定を選択する事は非常に重要になります。
全体像としては以下のように使い分けがなされます。
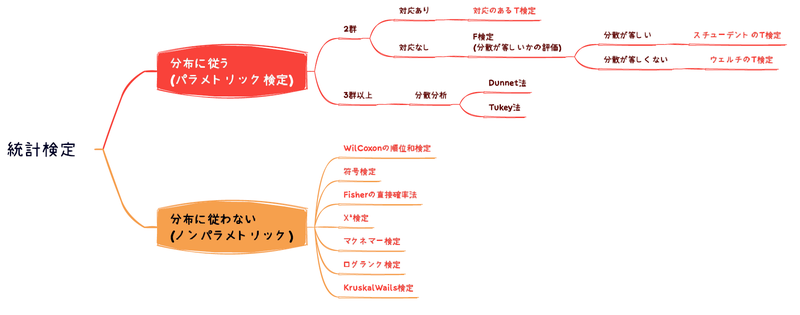
今後の記事で、使い分けの理由や検定ごとの検出力の違いについてなどご紹介していこうかと予定しております。
区間推定について
区間推定では、サンプルのでの結果から母集団における信頼範囲を推定する事を目的としています。
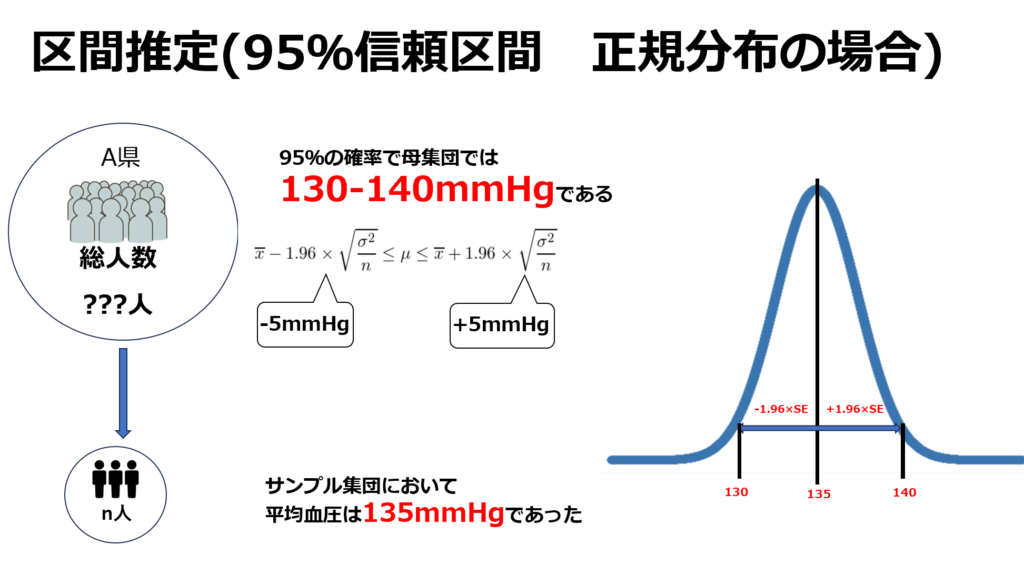
こちらも仮説検定同様にデータの性質に応じて算出に使用する式は変わってきます。
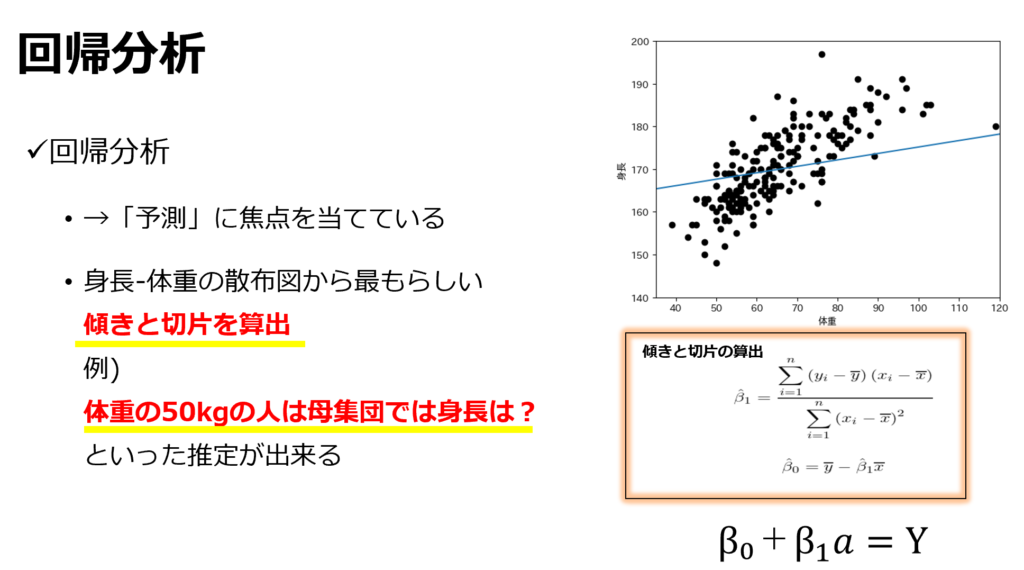
回帰分析
目的
回帰分析の目的は、「説明変数から母集団における目的変数の値を推測する事」になります。
説明変数が一つの時(単回帰分析)
単回帰分析では、1つの説明変数から1つの目的変数を推定します。例えば体重から母集団における身長を予測したい等です。
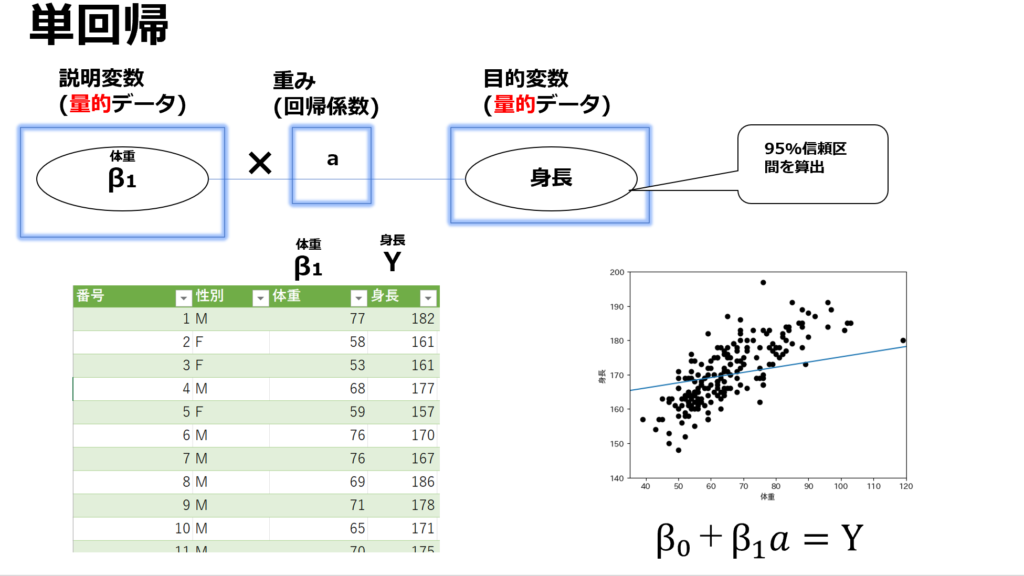
また、単回帰分析は原則として目的変数、説明変数共に量的データの時に行います。
説明変数が複数の時(重回帰分析)
複数の説明変数から一つの目的変数の推定を行いたい場合は「重回帰分析」を行います。単回帰分析同様に重回帰分析も原則として目的変数も説明変数も共に量的データの時に行います。
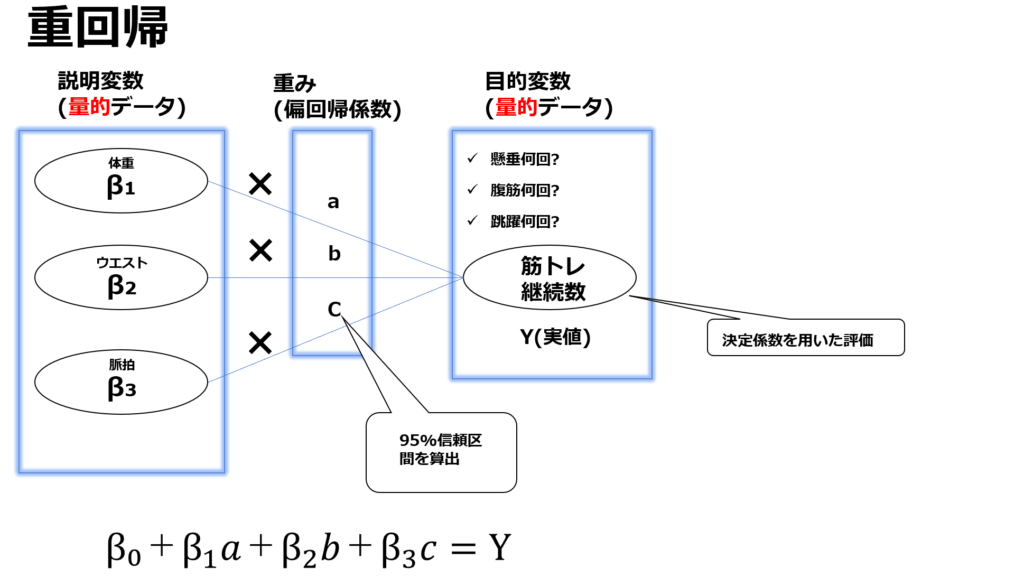
データの性質によっては、多重共線性(マルチコリニアリティ)が生じ偏回帰係数に大幅な誤差が生じる事があるので解釈には注意が必要になります。
目的変数が質的データの時(ロジスティクス回帰分析)
質的データの予測を行う際は、「ロジスティクス回帰分析」及び「ROC曲線によるカットオフ値の算出」を行います。ロジスティクス回帰ではY軸が対数値のため、0-1が目的変数の場合の間でその間の数値で算出されます。ロジスティクス回帰分析の出力値のうちカットオフ値以上であれば1と判定、カットオフ値以下であれば0と判定といった処理を行います。
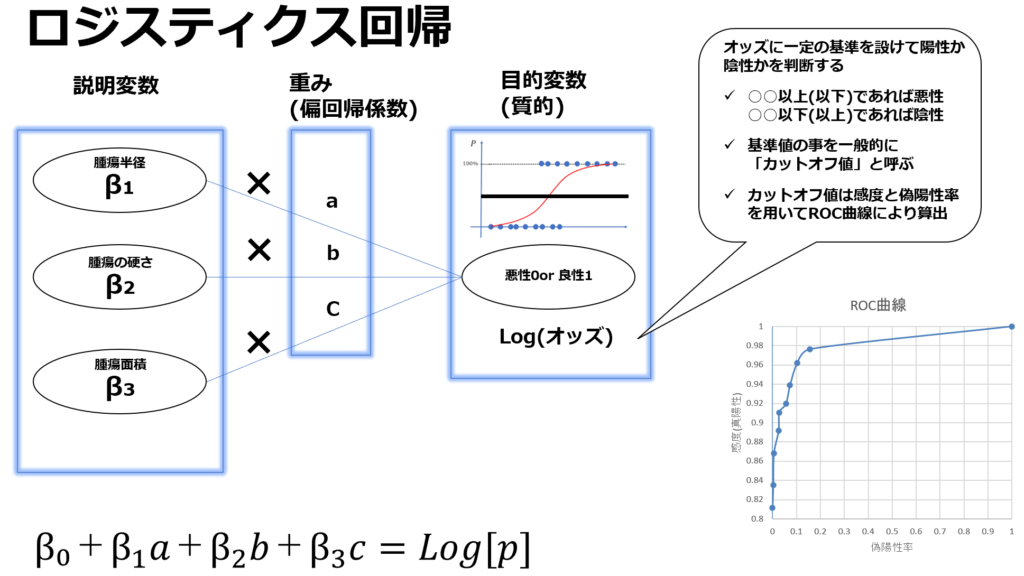
また、最適なカットオフ値を算出する手法がROC曲線による分析になります。
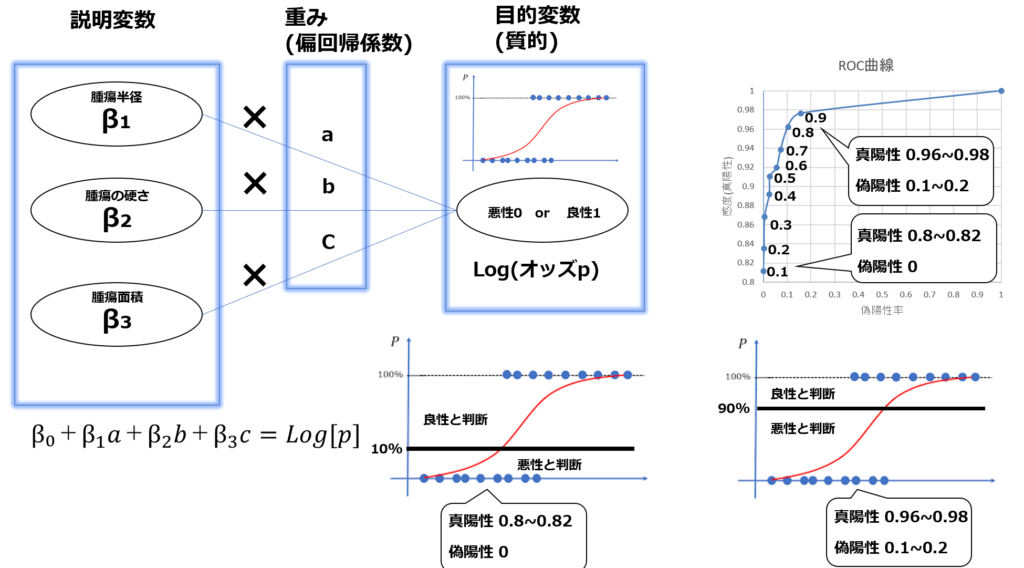
※おまけ: 多変量回帰分析の使い分け

まとめ
こちらが統計続編の記事になります!








コメント