初めに
記事の構成
- 添付文書や医療データを「正しく読み解く力」を身につけることができる
- 確率変数や確率分布の基本をわかりやすく学び、統計への苦手意識を克服できる
- 各種検定や区間推定を理解するために必要な「数学の基礎」をしっかり押さえられる
- 統計データを実務で役立てる具体的なヒントや考え方を学べる
分布を比較する上で必要になる考え方。
前回の記事では、添付文書に記載されたデータを例に、確率分布の種類と確率密度関数の基本を解説し、サンプルデータから母集団の特性を統計的に推定する方法を紹介しました。
今回は、2つのデータ群を比較する際に重要な「期待値」と「分散」の加法性・線形性について、わかりやすく解説します。
これを理解することで、次のような事が可能になります。
- 薬Aと薬Bの添付文書に記載された統計データを適切に比較・検定できる
- 複数の論文データを統計的に解釈し、エビデンスを正しく読み取れる
確率統計の基礎を押さえれば、医薬品データの正確な評価やエビデンスの適切な活用ができるようになります!
差の分布
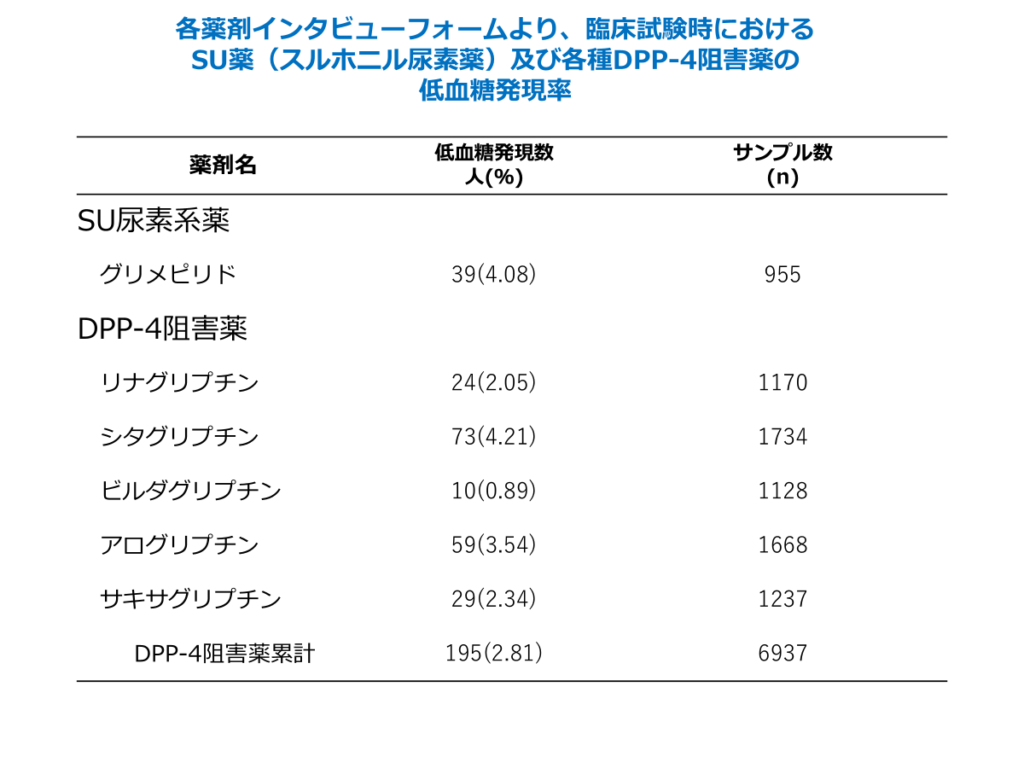
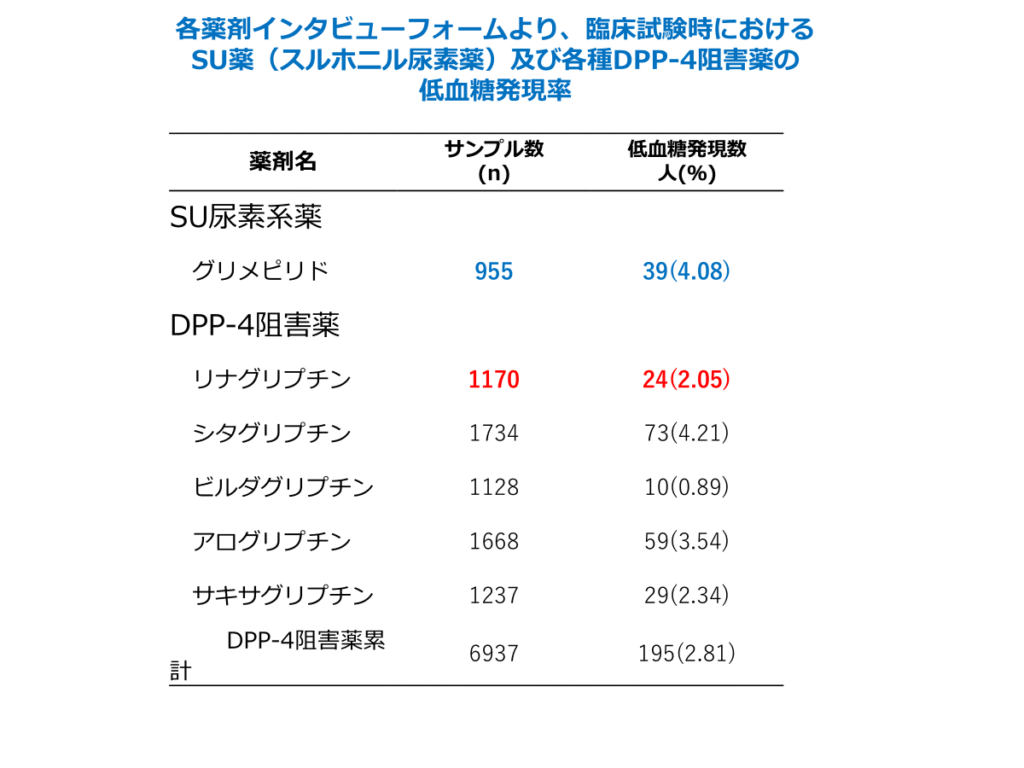
具体例として各種インタビューフォームに記載された、SU薬(スルホニル尿素薬)のグリメピリド投与群と比較した、各種DPP-4阻害薬の低血糖発現率を以下に示します。
このデータを用いて、「期待値」と「分散」の加法性・線形性をどのように活用できるのかを解説していきます。
具体的には、各群の低血糖発現率の期待値および分散を求め、期待値の差と分散の性質を活用することで、二項検定による有意差検定を実施することが可能になります。
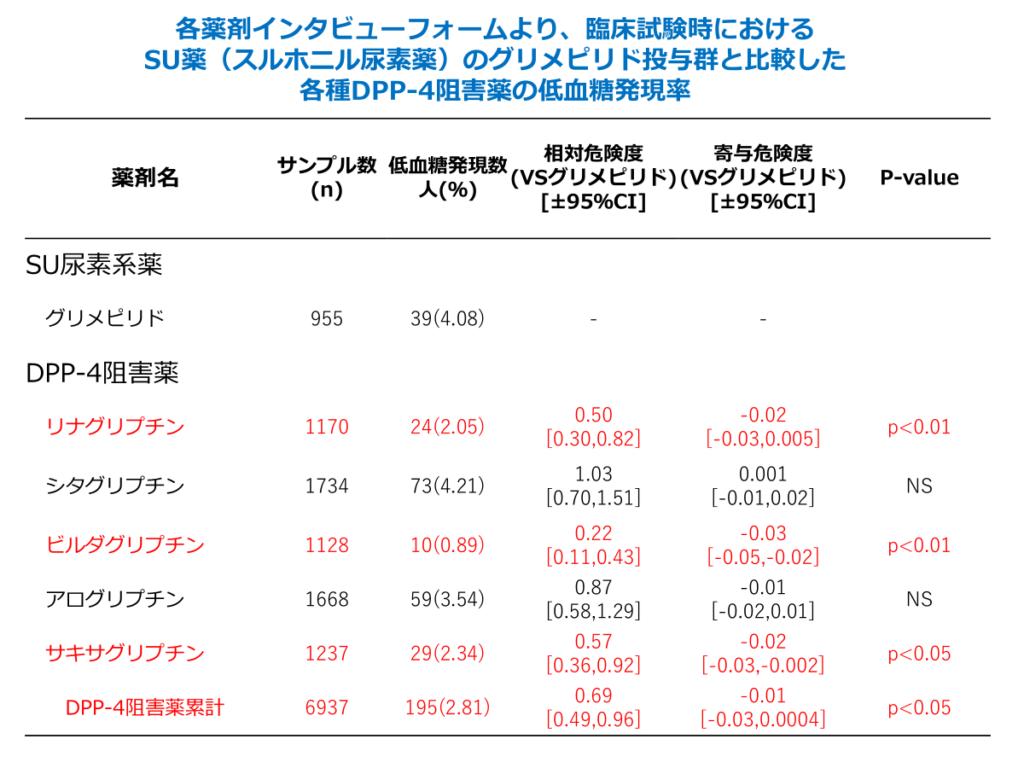
その結果、グリメピリドと比較した際の低血糖発現率について、以下のような統計的な有意差が確認されました。
- リナグリプチン、ビルダグリプチン → 有意水準 0.01(p < 0.01)で 有意に低血糖発現率が低い
- サキサグリプチン、DPP-4阻害薬全体 → 有意水準 0.05(p < 0.05)で 有意に低血糖発現率が低い
期待値の加法性と分散の性質を活用することで、単なる数値比較ではなく、統計的に信頼性の高い評価が可能になります!
期待値、分散、共分散の性質
期待値、分散、共分散とは
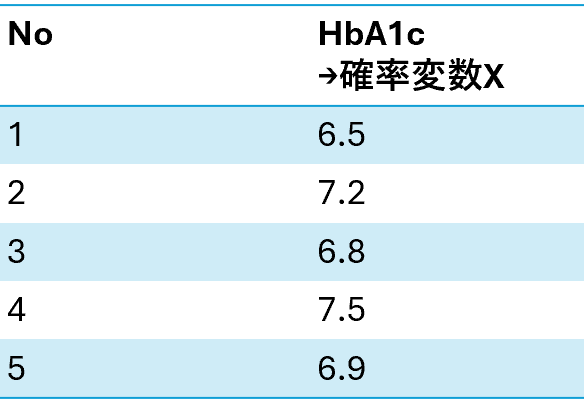
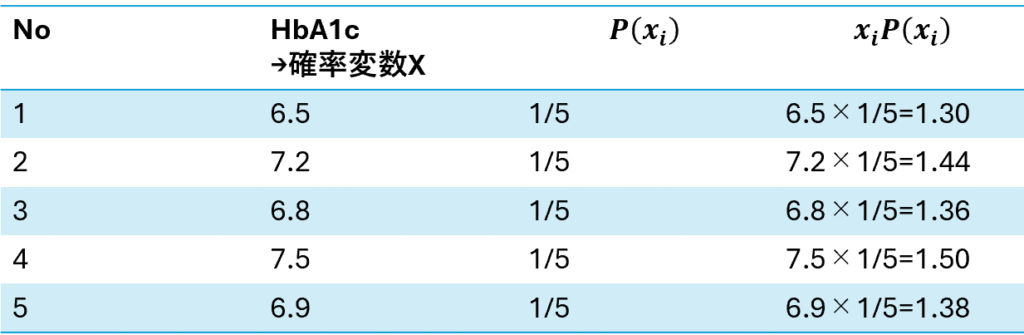
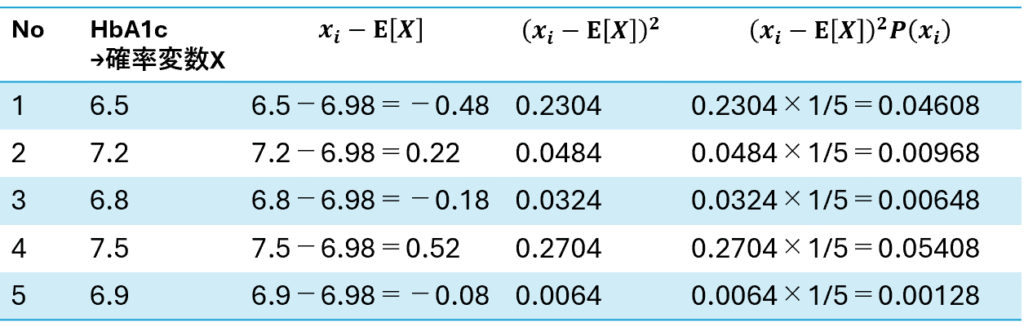
サンプルデータとして以下のデータを想定します。患者5名分のHbA1cのデータがあります。これを基に期待値・分散を考えてみます。
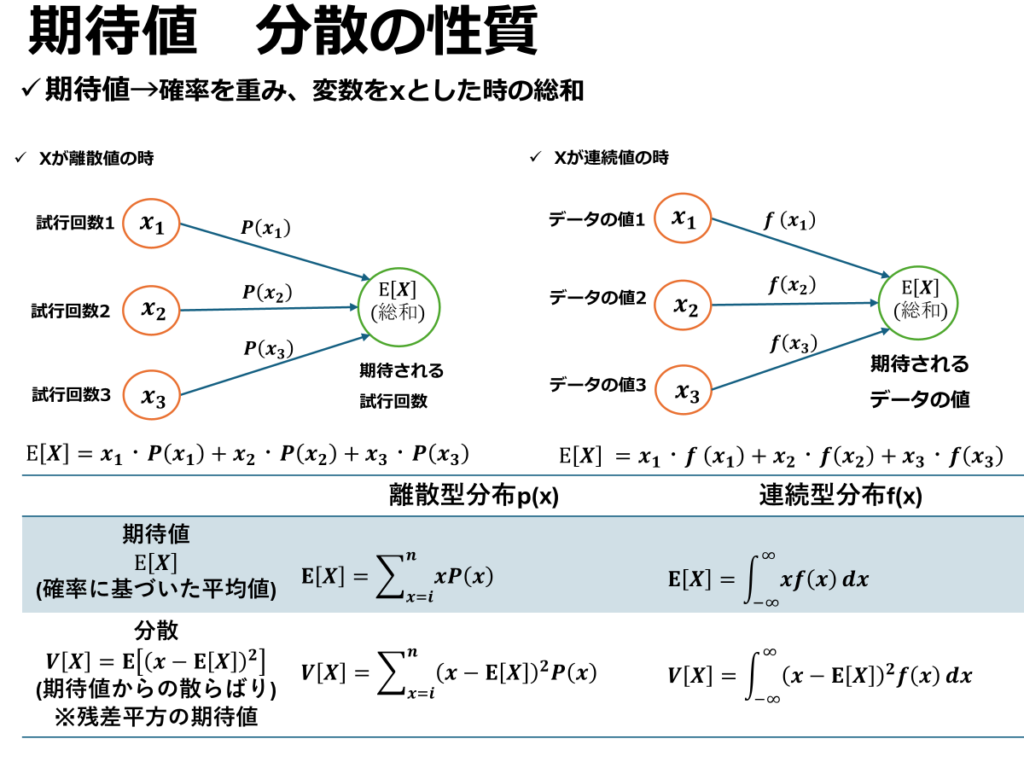
期待値とは
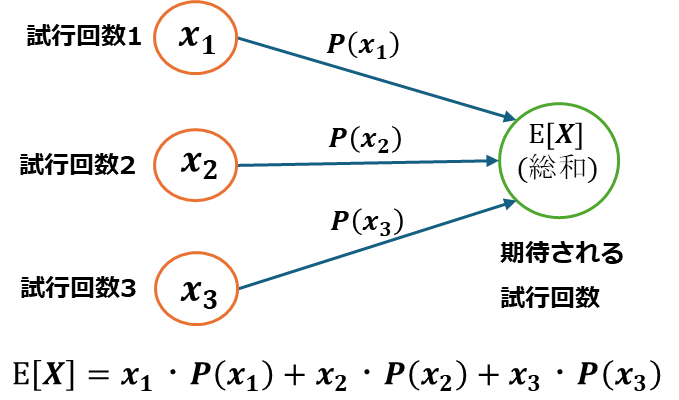
期待値とは、得られ得る全ての確率変数と、それが起こる確率密度の積を足し合わせたものになります。例えば離散型確率変数x1,x2,x3があり、それが起こる確率がp(x1),p(x2),p(x3)であるとします。
よってXの期待値は以下の式で表せます
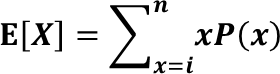
連続型確率変数でも同様です
連続データx1,x2,x3があり、その確率密度がそれぞれf(x1),f(x2),f(x3)であるとします。
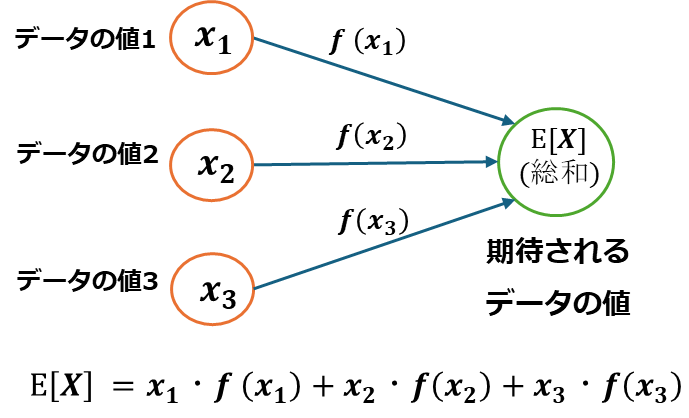
よってXの期待値は以下の式で表せます
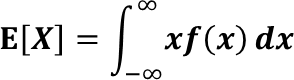
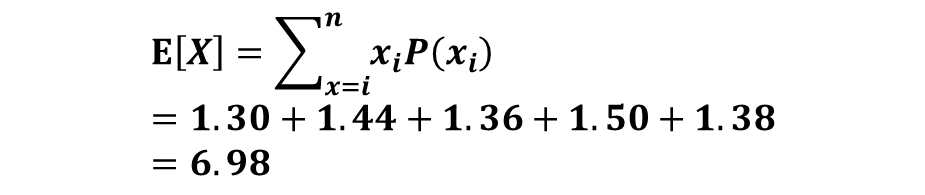
分散とは
分散とは、各確率変数の偏差平方和(値と期待値の差の値を2乗した値)の期待値になります。例えば離散型確率変数x1,x2,x3があり、それが起こる確率がp(x1),p(x2),p(x3)であるとします。
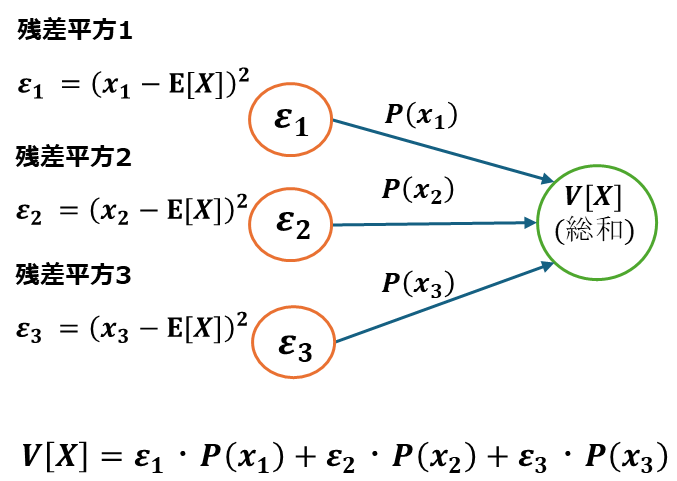
よってXの分散は以下の式で表されます。
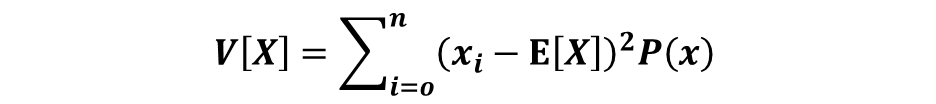
連続型確率変数でも同様です
連続データx1,x2,x3があり、その確率密度がそれぞれf(x1),f(x2),f(x3)であるとします。
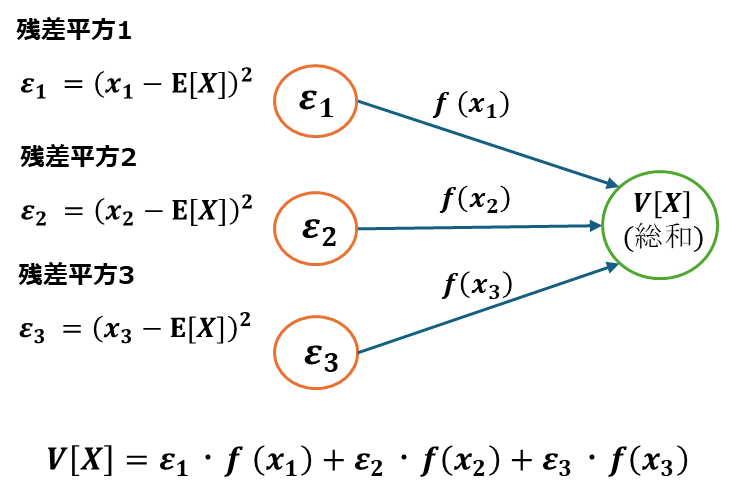
よってXの分散は以下の式で表されます。
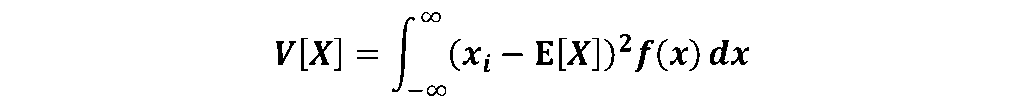
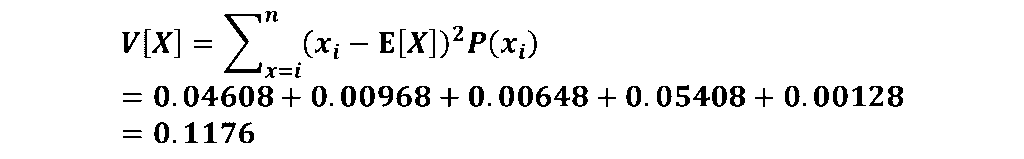
共分散とは
共分散とは、2つのデータが「一緒にどれくらい動くか」を数値で表したものです具体的には、対応する2つの確率変数 XとYの偏差(平均からのずれ)の積の期待値として定義されます。
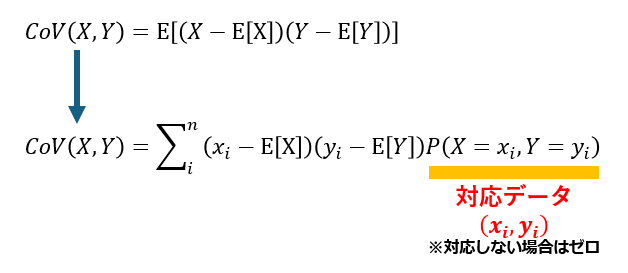
共分散が0になるのは、XとYの偏差の積の期待値が0、つまりXとYの間に線形な関係がない場合です。
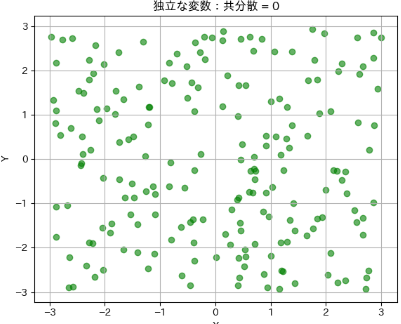
また、XとYが独立である場合も、共分散は必ず0になります。
これは、独立であれば一方の値が他方に全く影響を与えないため、偏差の積の期待値も0になるからです。
一般的に、共分散は「XとYが同じ対象(たとえば同じ人、同じ時間点など)に関する2つのデータ」で計算します。これを「XとYが対応している」といいます。
一方で、「XとYが対応していない」──たとえば、まったく別々の人から取ったデータ──では、そもそも共分散を計算する意味がありません。
このような関係性のないXとYは、ある意味で独立と考えることもできます。
ただし、統計学で「独立」とは、XとYが確率的に互いに影響しない関係を意味します。
「対応していない」ことと「独立である」ことは似ているようで、意味は異なります。
このため共分散が0だからといって、必ずしもXとYが独立とは限りません。
非線形な関係をもつ変数同士では、独立ではないのに共分散が0になることもあります。
- 正の共分散 → 一方が増えるともう一方も増える傾向(同じ方向に動く)
- 負の共分散 → 一方が増えるともう一方は減る傾向(逆方向に動く)
- 0に近い共分散 → 変数同士にほとんど関係がない(独立とは限らない)
たとえば、以下のようなケースが考えられます。
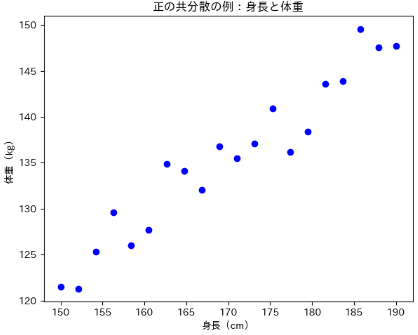
正の共分散の例
「身長」と「体重」
→ 一般的に、身長が高くなると体重も増える傾向があるため、共分散は正になります。
負の共分散の例
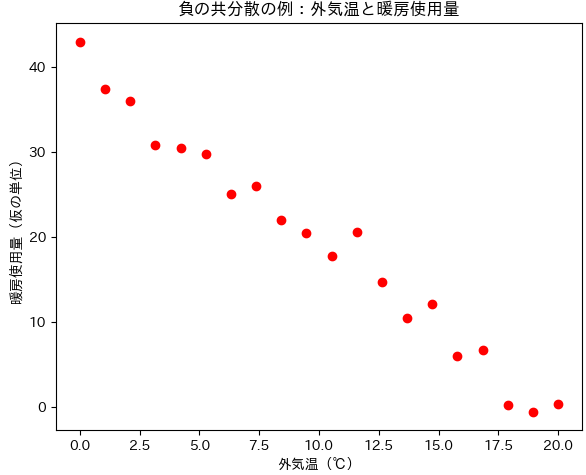
「外気温」と「暖房の使用量」
→ 外の気温が上がると暖房の使用量は減る傾向があります。このように、一方が増えるともう一方が減る関係では、共分散は負になります。
期待値、分散の加法性
期待値の加法性
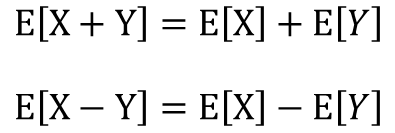
二種類の確率変数XとYがあるものとします。この時、X+Yの期待値はXの期待値とYの期待値を足したものに、X-Yの期待値はXの期待値からYの期待値を引いたものになります。
以下がX+Yの期待値の加法性に関する証明になります。分配法則を用いる事で簡単に導出できます。ただし、以下の式はXとYが対応した変数であると仮定して導出を行っております。
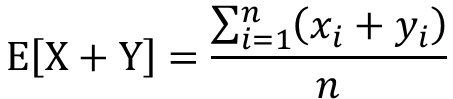
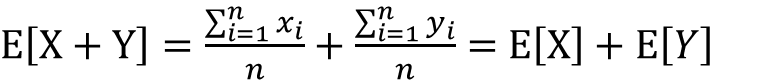
また、上記の加法性は、XとYが対応していなくても成り立ちます。この理由については、同時確率密度関数などの知識が必要になりますので後日別の記事で紹介する予定です。
以下をXとYの同時確率密度関数であるとします。
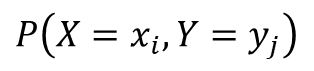
この時、XとYの和の期待値は以下のように導出されます。

分散の加法性
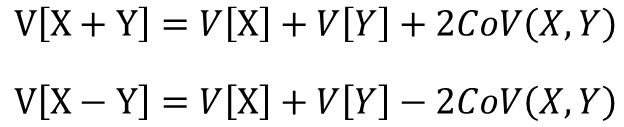
確率変数XとYが独立である場合、共分散Cov(X,Y)はゼロになる為
※共分散については後述
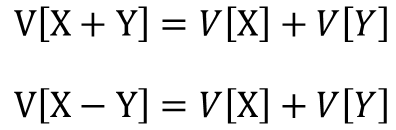
分散の加法性(加算)
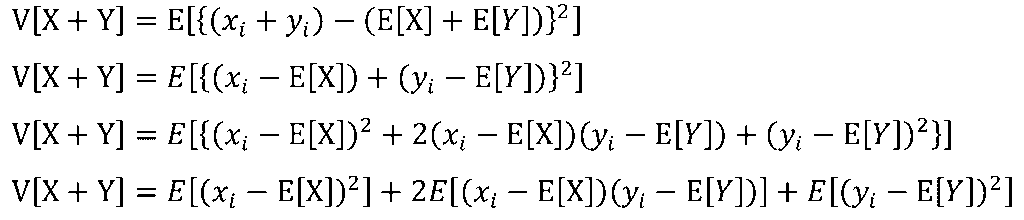
分散の加法性(減算)
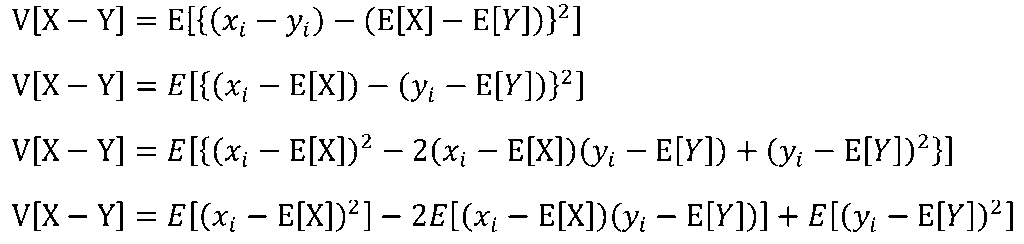
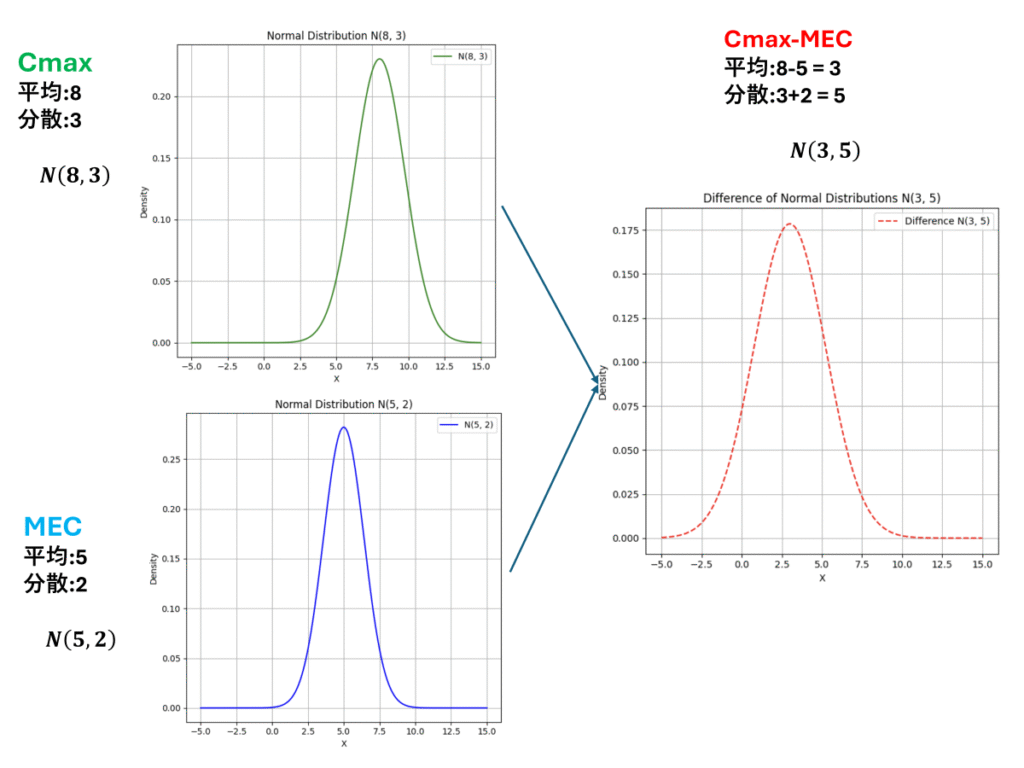
期待値・分散の加法性 活用例(薬物動態学)
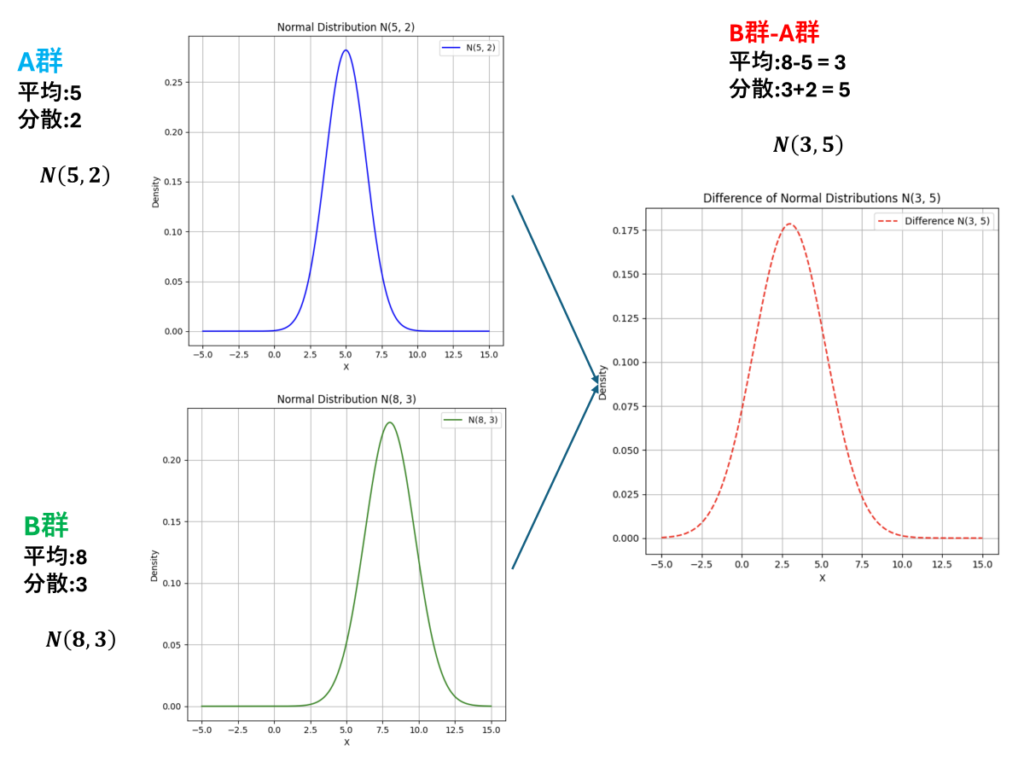
ある薬物が体内に投与されたとき、血中濃度のピーク値(Cmax)は期待値8分散3の正規分布 に従うと報告されています(単位:μg/mL)。一方で、この薬物の最小有効濃度(MEC)は個人差により 期待値5分散2の正規分布 に従うとされています(単位:μg/mL)。
このとき、ランダムに選ばれた患者について、CmaxからMECを引いた差の値の分布はどのようになるでしょうか?
期待値の加法性より
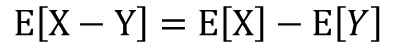
8-5=3
よって期待値は3となります。
分散の加法性より
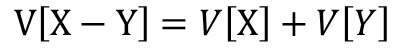
3+2=5
分散は5となります。
Cmax-MEC(最高血中濃度が)患者に必要な最小濃度を度程度上回っているか?を示す値です。この値は平均3 分散5の正規分布に従う事がわかりました。
この事からこの薬は平均して3μg/mLの余裕があるが、ばらつきが5とやや大きめと解釈する事が出来ます。
期待値、分散の線形性
期待値・分散の加法性の一般化
線形性の説明に入る前に、加法性の一般化について触れます。
期待値の加法性の一般化
確率変数X1とX2の和の期待値は加法性より以下の様に表されます。
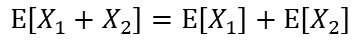
ここにX3を加えた場合も同様に以下の式が成り立ちます。
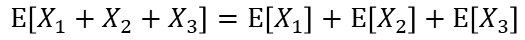
確率変数がX1,X2,X3・・・Xnとn個ある場合の確率変数の総和の期待値は以下のように一般化されます。
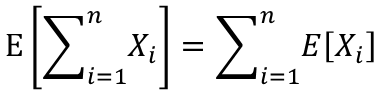
分散の加法性の一般化
確率変数X1とX2の和の分散は加法性より以下の様に表されます。
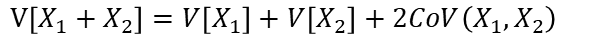
ここにX3を加えた場合も同様に以下の式が成り立ちます。
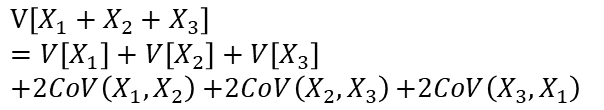
ここにX4を加えた場合も同様に以下の式が成り立ちます。
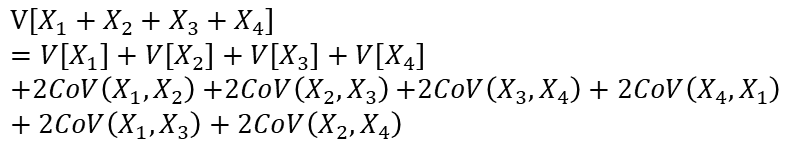
確率変数がX1,X2,X3・・・Xnとn個ある場合の確率変数の総和の分散は以下のように一般化されます。
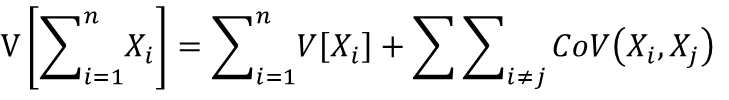
期待値の線形性
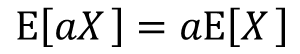
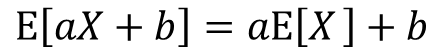
確率変数Xについて考えます。この時、aX、aX+bの期待値は上記の式で表す事が出来ます。
まずは切片無しの場合から証明していきます。
期待値の定義よりE[aX]は以下の式で表せます

分配法則によりaをくくりだすことが出来ます。
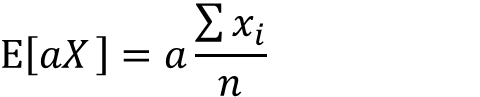
分数部分はxの期待値として表せます。
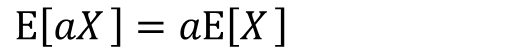
これは、同様の確率変数Xをa個足した時の確率変数の加法性として考える事も出来ます。
aXiが成り立つ時 X1=X2=X3=Xi
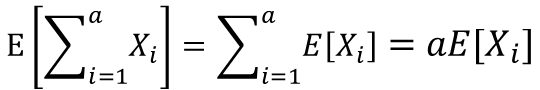
切片がある場合も同様です。
期待値の定義よりE[aX+b]は以下の式で表せます
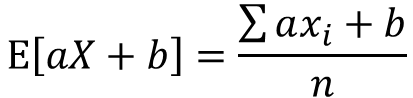
分配法則よりaはくくり出し、bは定数の為n倍になります。
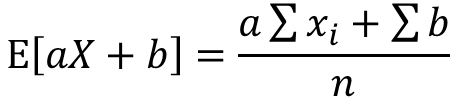
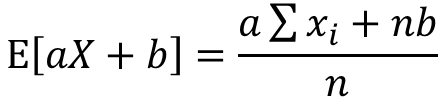
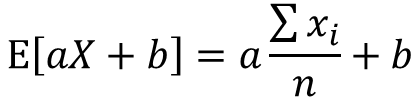
分数部分はxの期待値として表せます。
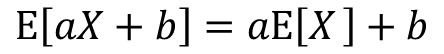
分散の線形性
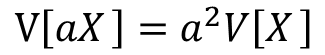
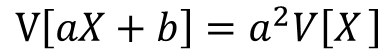
確率変数Xについて考えます。この時、aX、aX+bの分散は上記の式で表す事が出来ます、
まずは切片無しの場合から証明していきます。
分散の定義よりV[aX]は以下の式で表せます
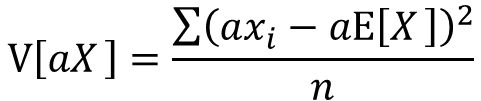
分配法則によりaの2乗をくくりだすことが出来ます。
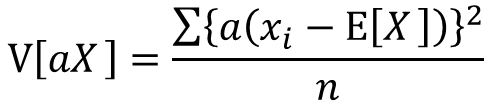
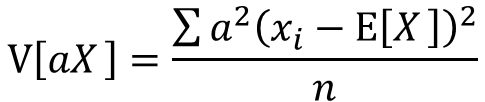
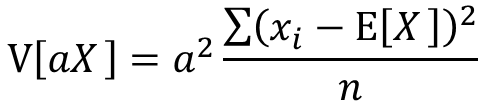
分数部分はxの分散として表せます。
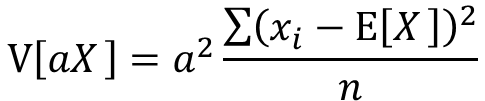
xの分散の定義より以下の式が成り立ちます。
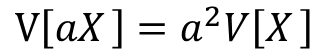
これは、同様の確率変数Xをa個足した時の確率変数の線形性として考える事も出来ます。
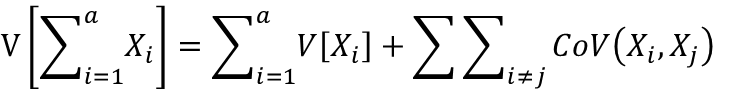
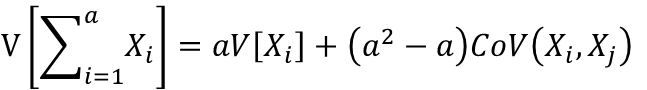
aXiが成り立つ時 X1=X2=X3=Xiの場合、V(Xi)=CoV(Xi,Xj)になるため
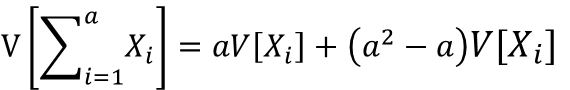
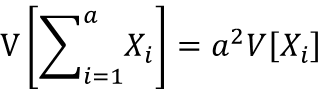
切片がある場合も同様です。
分散の定義よりV[aX+b]は以下の式で表せます
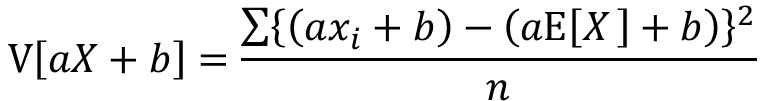
分配法則によりaの2乗をくくり出します。また、bは式変形により消えます。
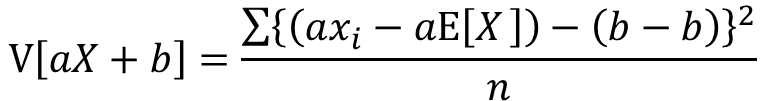
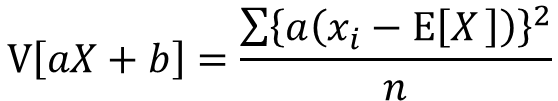
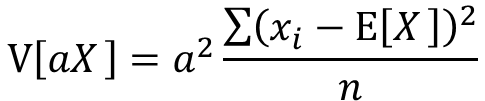
xの分散の定義より以下の式が成り立ちます。
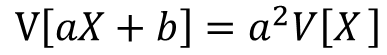
期待値・分散の線形性の活用例
期待値、分散の線形性の活用事例を考えてみます。薬剤の血中濃度Xと効果Yの間に以下のような線形関係がみられることが分かっていると仮定します。この場合、Xの期待値・分散とYの期待値・分散の間には以下の関係が成立します。

確率変数の標準化
Z統計量(標準正規分布)
標準化とは期待値0、標準偏差が1となるように確率変数の値を調整する事を指します。これにより、異なる期待値と分散をもつデータであってもその大小関係を比較することが可能になります。
確率変数Xの期待値をE[X]、分散をV[Y]とします。そして、Xは以下の式で標準化されます。標準化された確率変数をZとおきます。
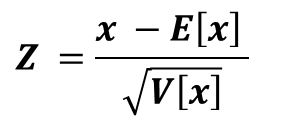
期待値の線形変換の性質より、Zの期待値は0になります。
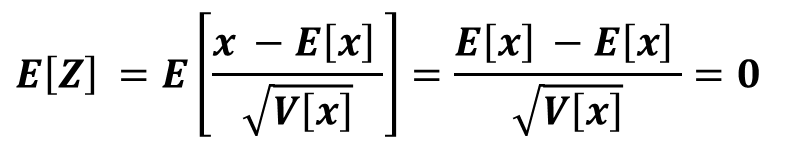
分散の線形変換の性質より、Zの期待値は0になります。
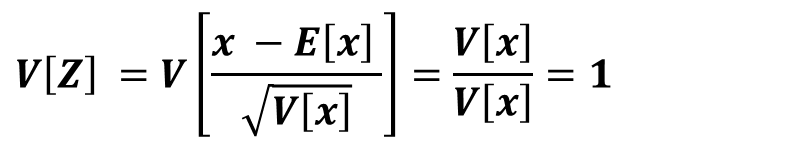
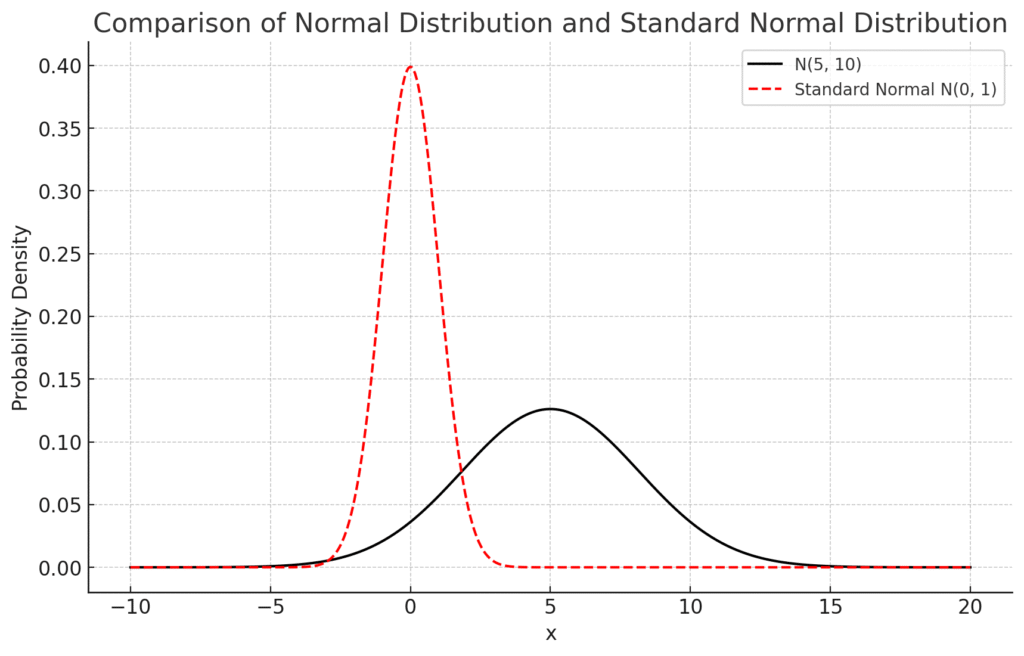
上のグラフでは、黒い線が平均5・分散10(標準偏差√10)の正規分布 赤い破線が平均0・分散1の標準正規分布 を表しています。
このように、元の正規分布に対して標準化(Z変換)を行うことで、すべてのデータを「平均0・分散1」に揃えることができます。これによって、異なる分布同士の比較や、統一的な分析がしやすくなります。
数学と組み合わせて一歩先の理解を
二項分布の期待値と分散
最後に二項分布の正規近似に触れます。これを理解する事で、冒頭にお示しした以下の比較データについての理解に繋がります!
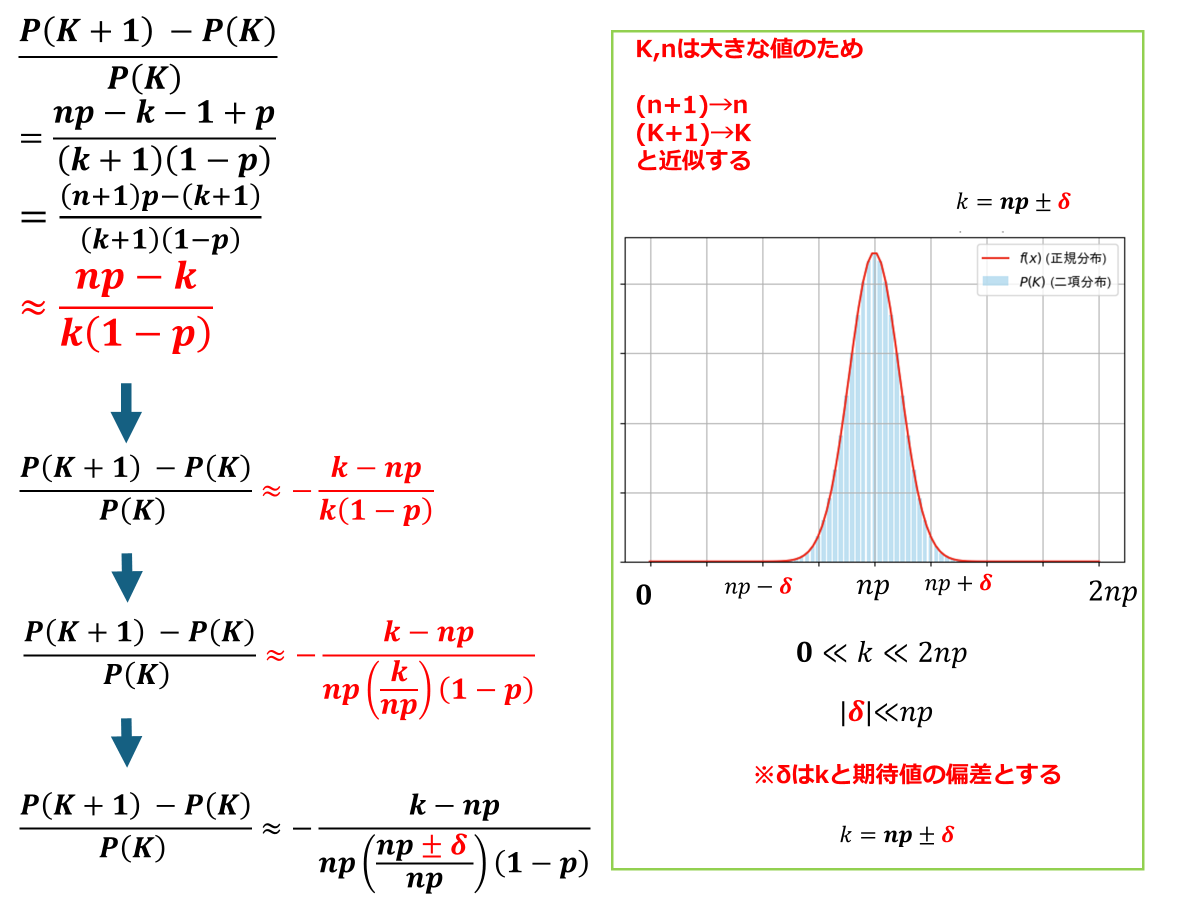
二項分布は、確率pの事象をn回繰り返したとき、その発生数が従う分布であり、確率密度関数は以下の式で表せます。
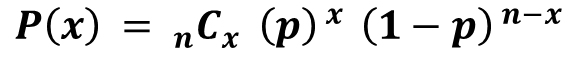
二項分布の期待値はnp、分散はnp(1-p)で表せます。
対して正規分布とは、連続型確率変数が一般的に従う分布で、最頻値・期待値・中央値が一致する左右対称の分布になります。確率密度関数は以下の式で表せます。
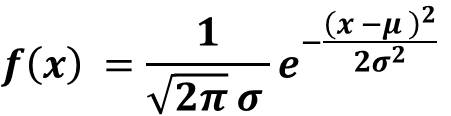
正規分布の期待値はμ、分散はσ^2で表せます。
二項分布の期待値と分散の証明
二項分布の期待値を導出していきます。


以上より二項分布の期待値E[X]はnpで表せる事を証明出来ました。
次に分散を導出していきます。まずは下準備が必要になります。
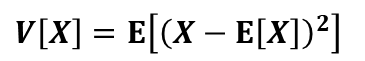
分散の定義の式を以下のように式変形して
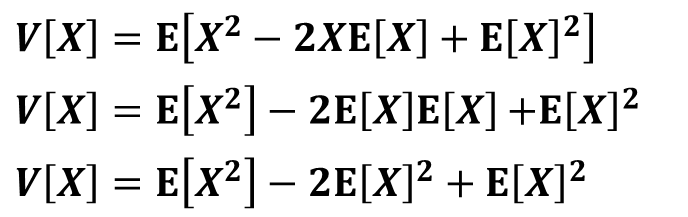
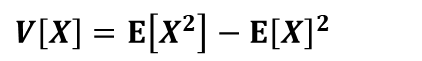
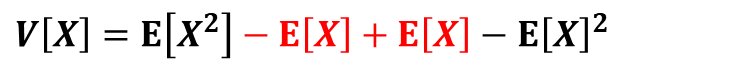
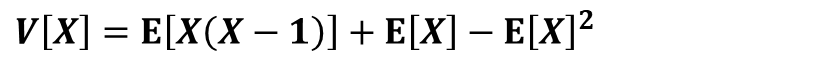
E[X(X-1)]の項については確率密度関数を用いて、それ以外の項については期待値E[X]=npを代入する形で計算を進めていきます。

計算過程は以下に続きます。
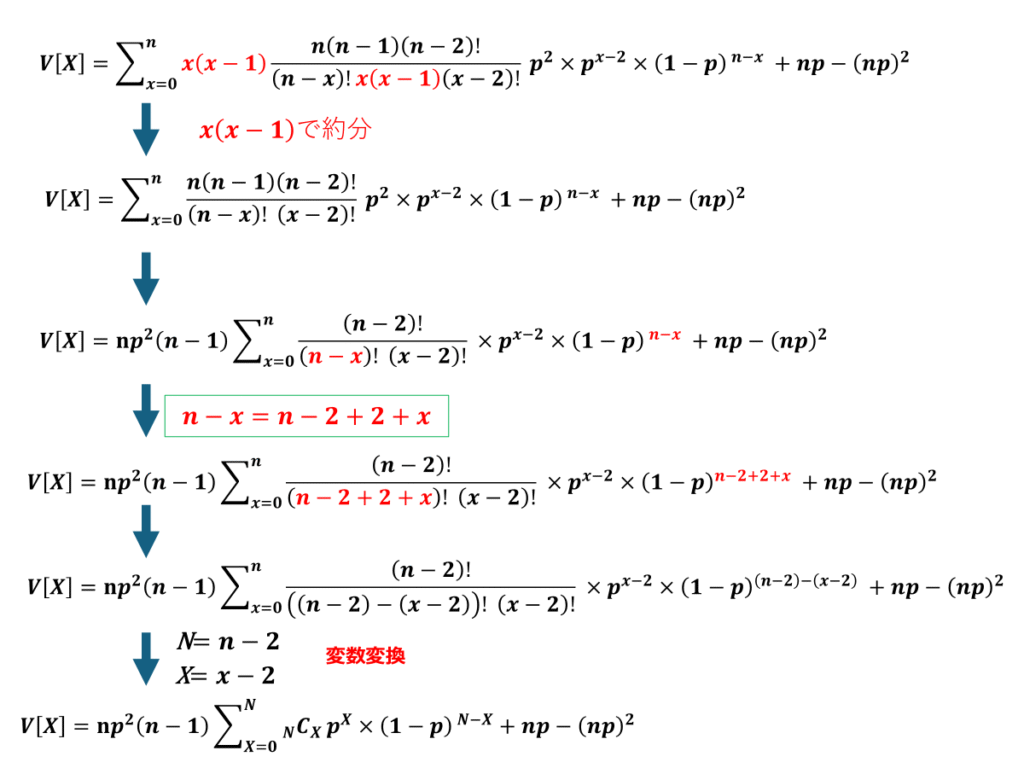
計算過程は以下に続きます。
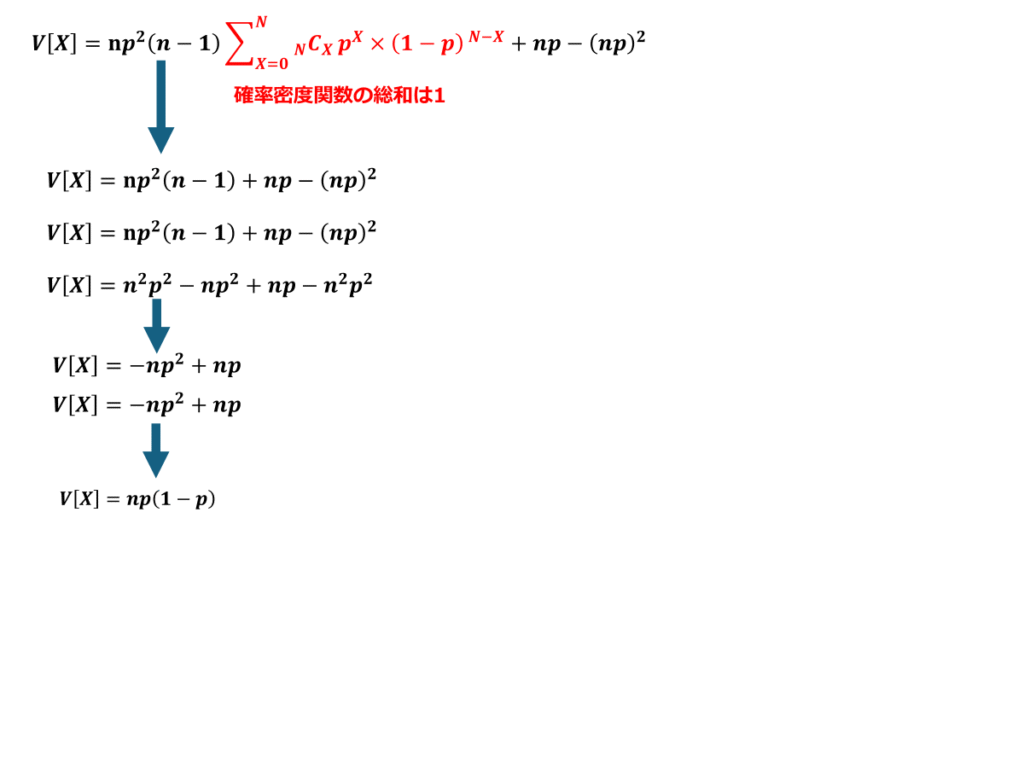
以上より二項分布の期待値V[X]はnp(1-p)で表せる事を証明出来ました
正規分布の期待値と分散の証明
次に、正規分布の期待値と分散について触れます。ここでは正規分布の確率密度関数を期待値及び分散の定義に代入し、そこに含まれるパラメータμが期待値に、パラメータσの2乗が分散に一致する事を証明していきます。
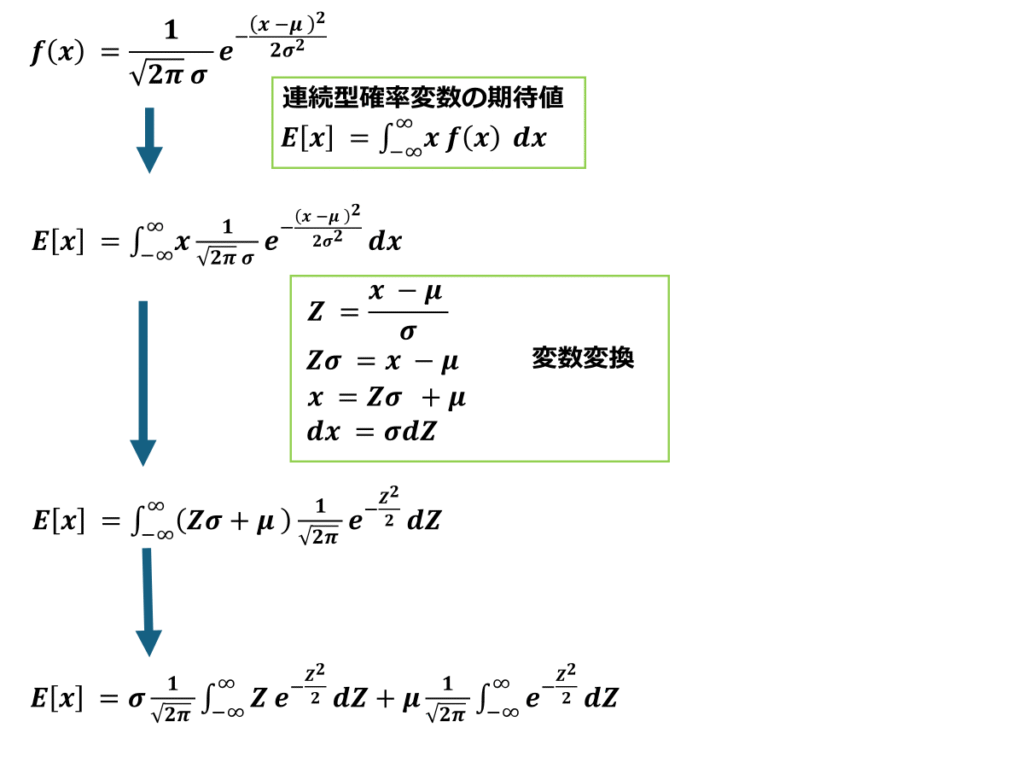
計算過程は以下に続きます
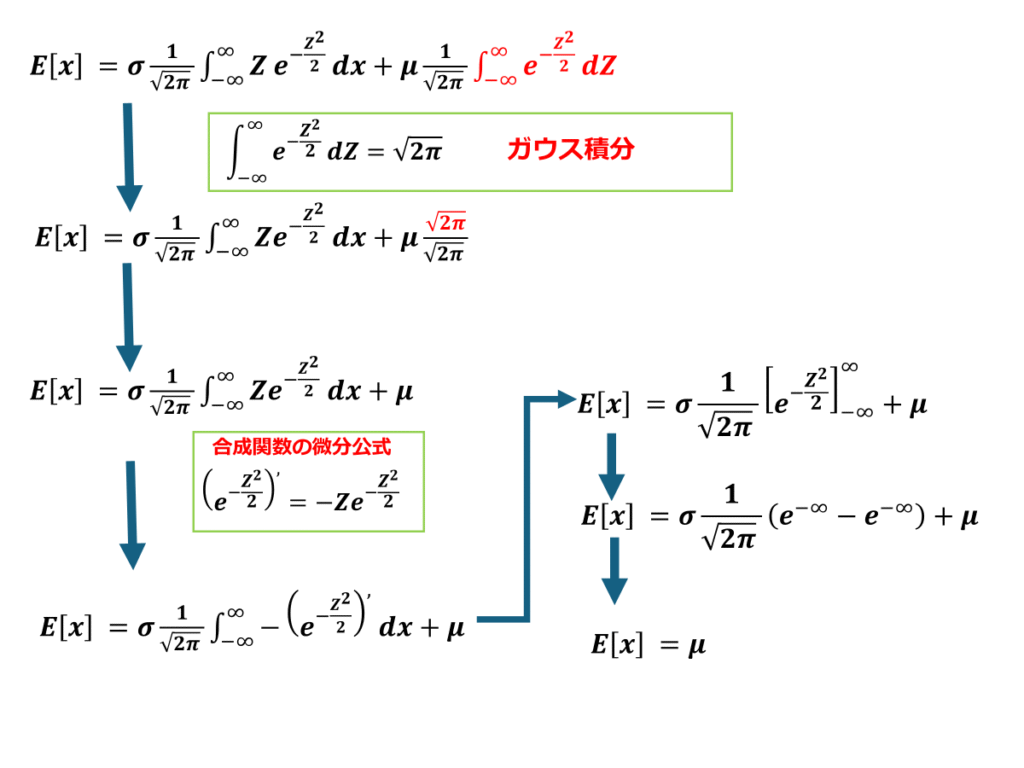
以上より正規分布の期待値はμであることを証明できました。
※正規分布の期待値と分散の証明式を導出する
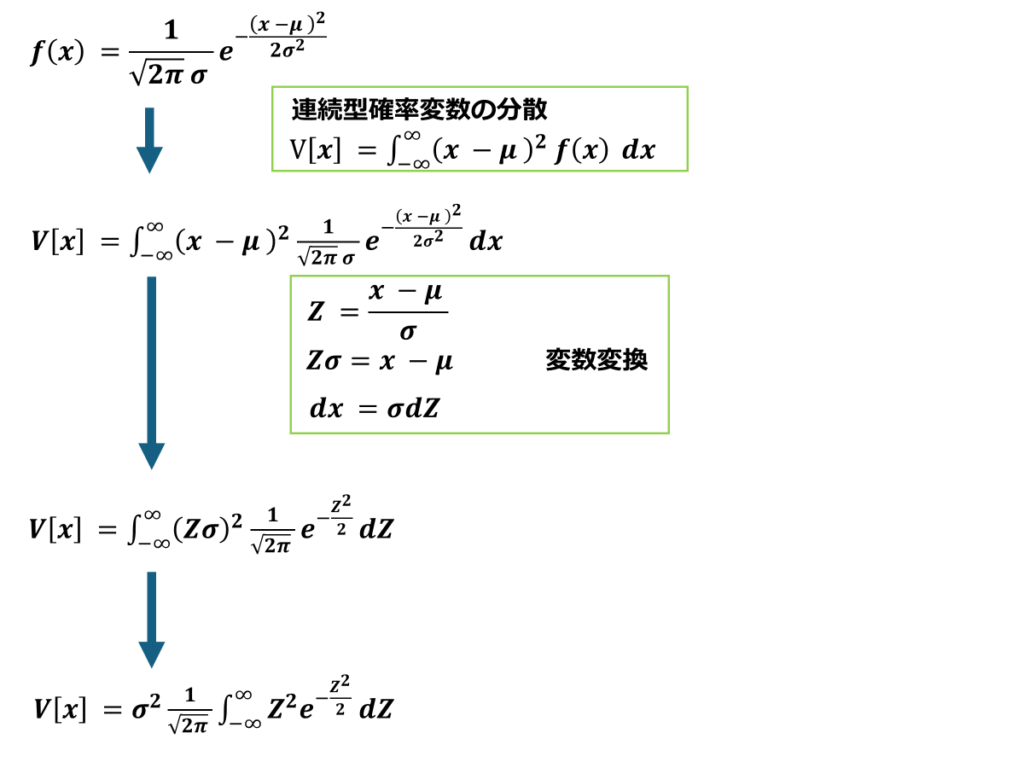
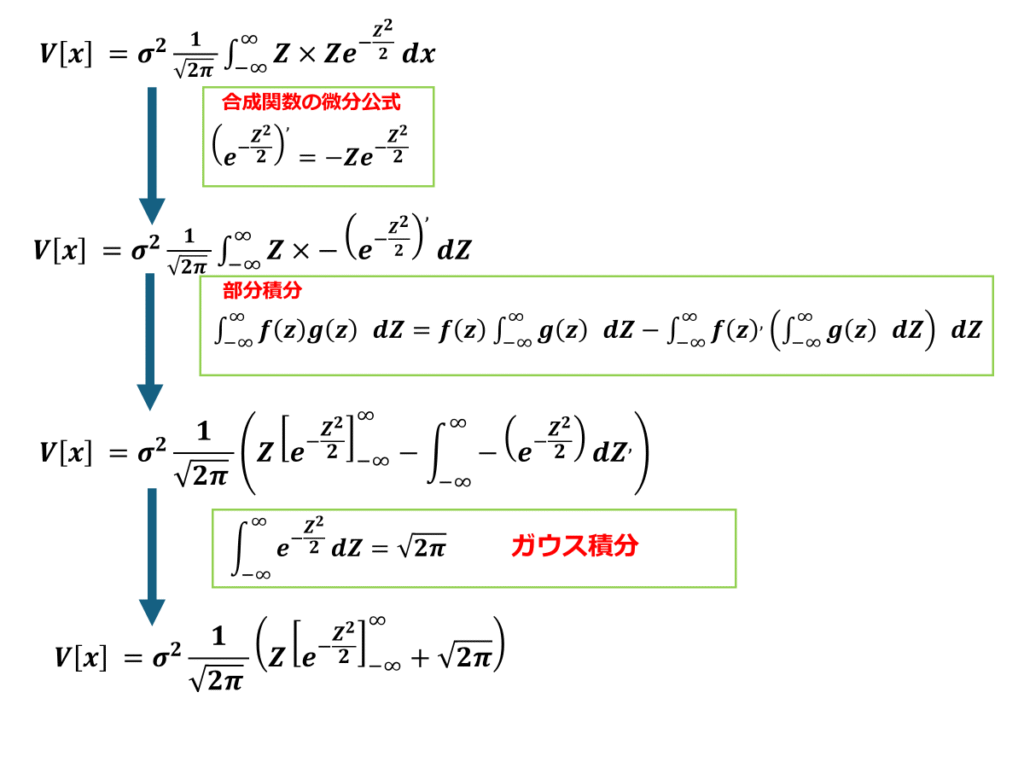
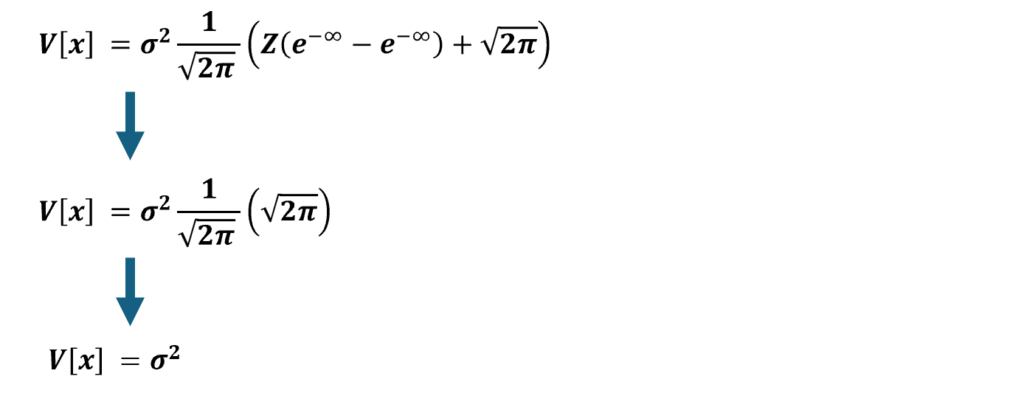
以上より正規分布の分散はσ^2であることを証明できました。
二項分布から正規分布へ
これまで二項分布及び正規分布の期待値及び分散に触れました。これを基に、np=μ、np(1-p)=σ^2と変数変換を行った上、n→∞に増やしていった場合の極限を取る事で二項分布から正規分布に近似する事が可能になります。
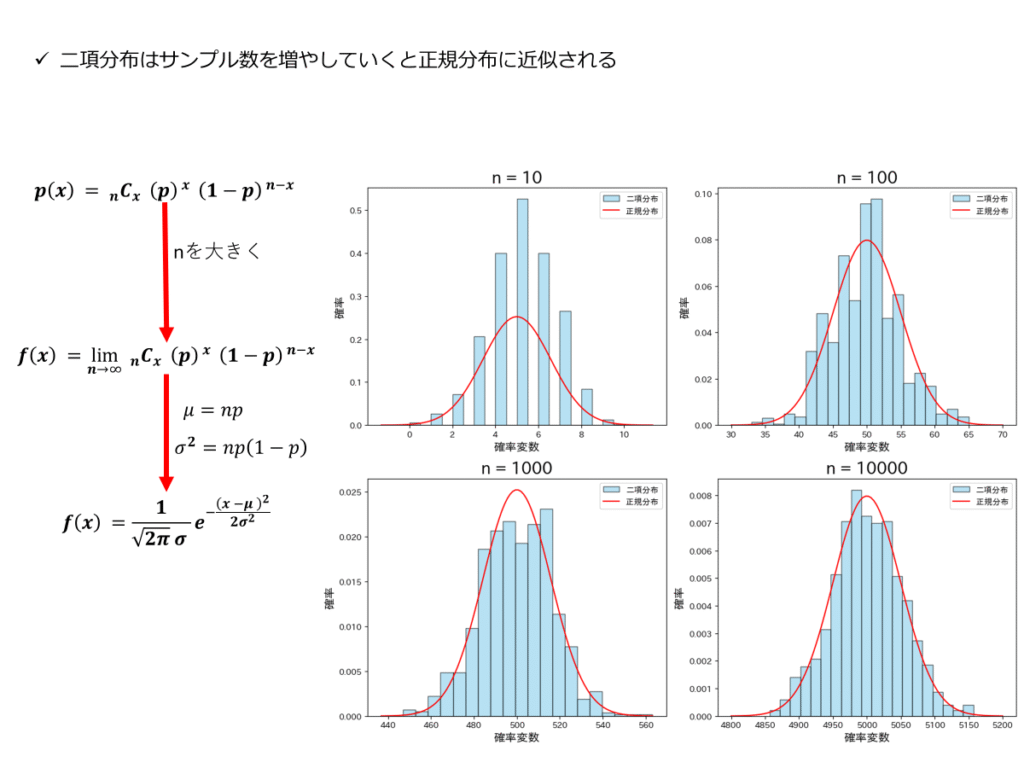
二項分布の確率密度関数から正規分布の確率密度関数を導出していきます。
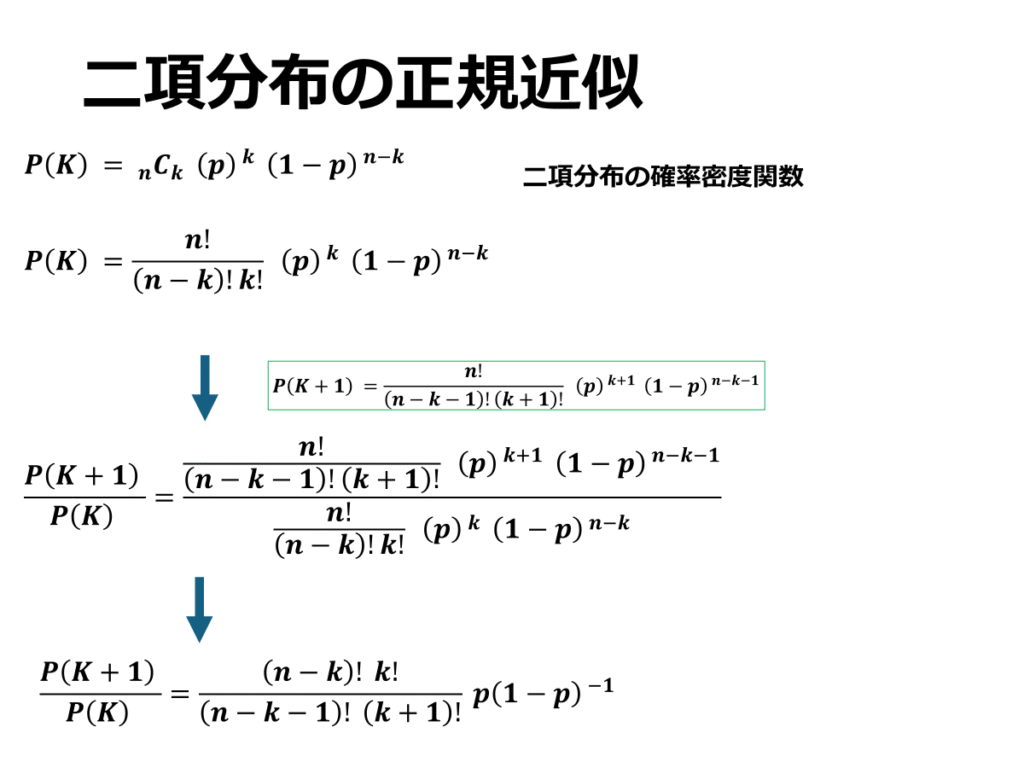
計算過程は以下に続きます。
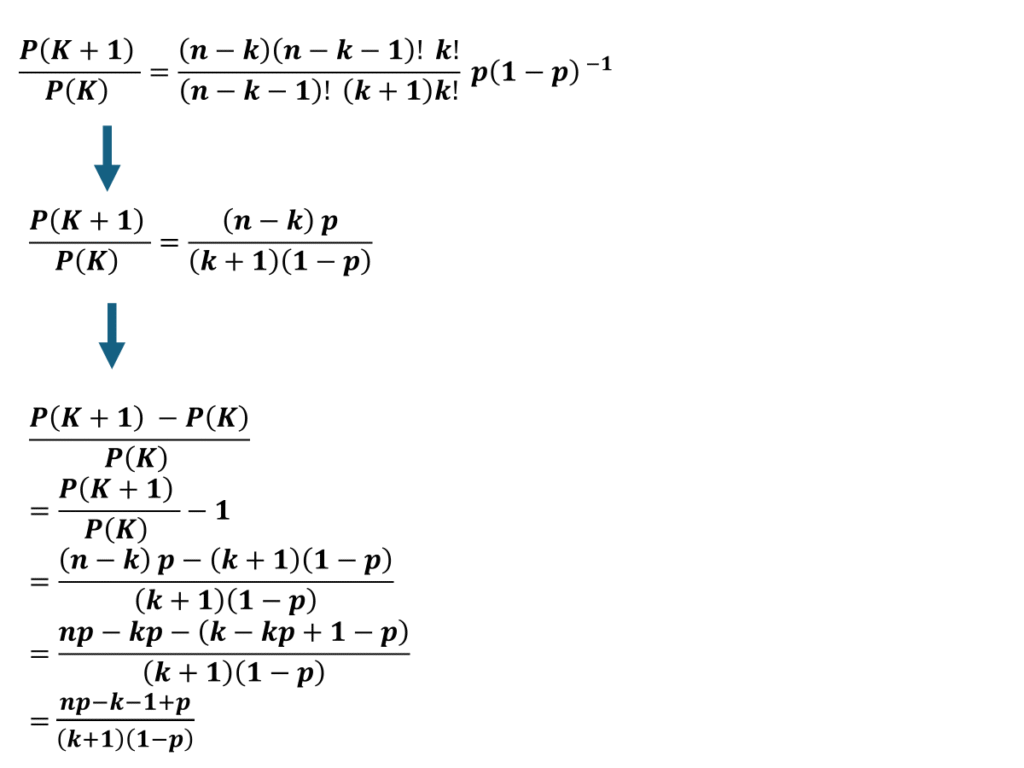
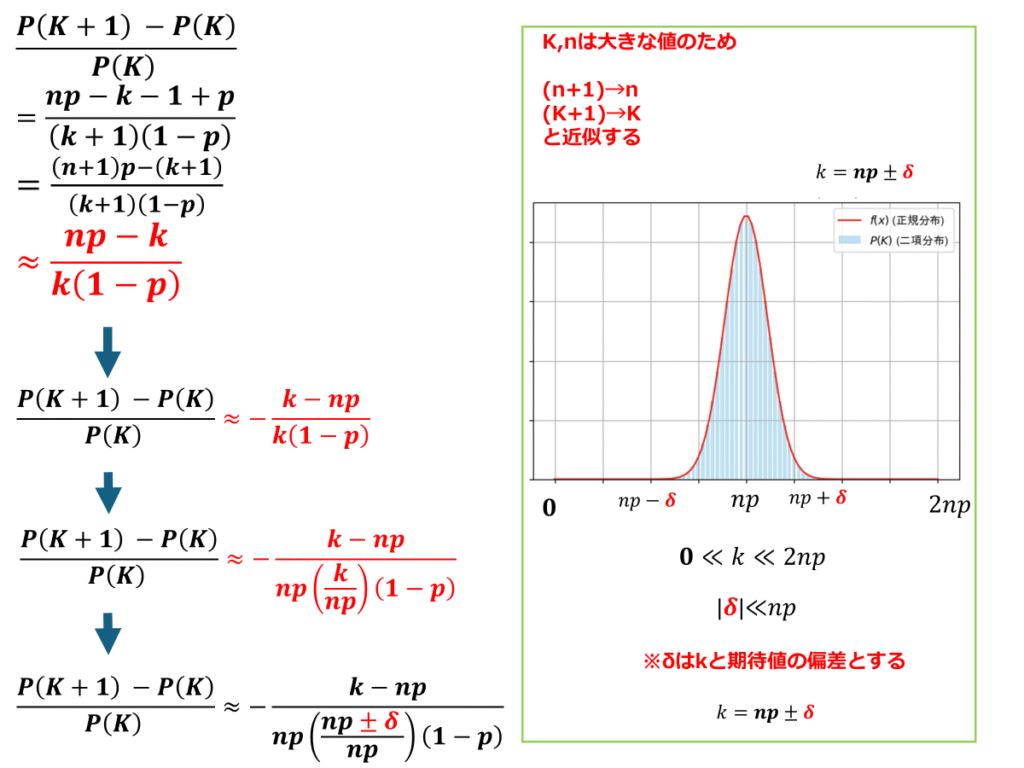
計算過程は以下に続きます。
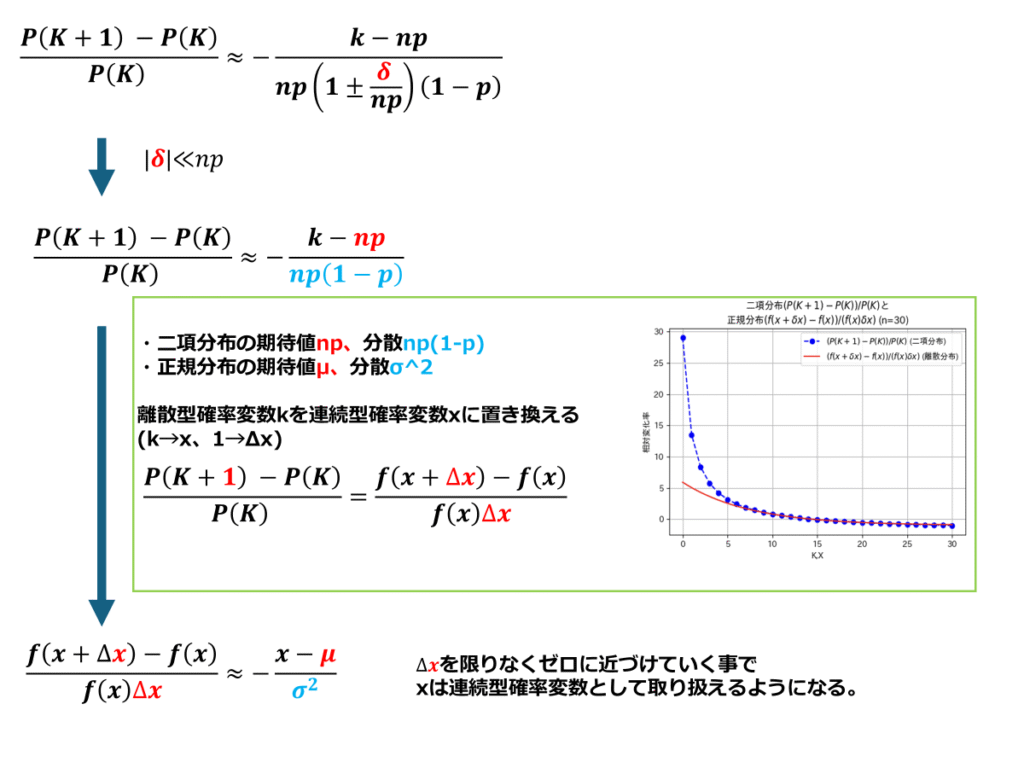
計算過程は以下に続きます。

計算過程は以下に続きます。
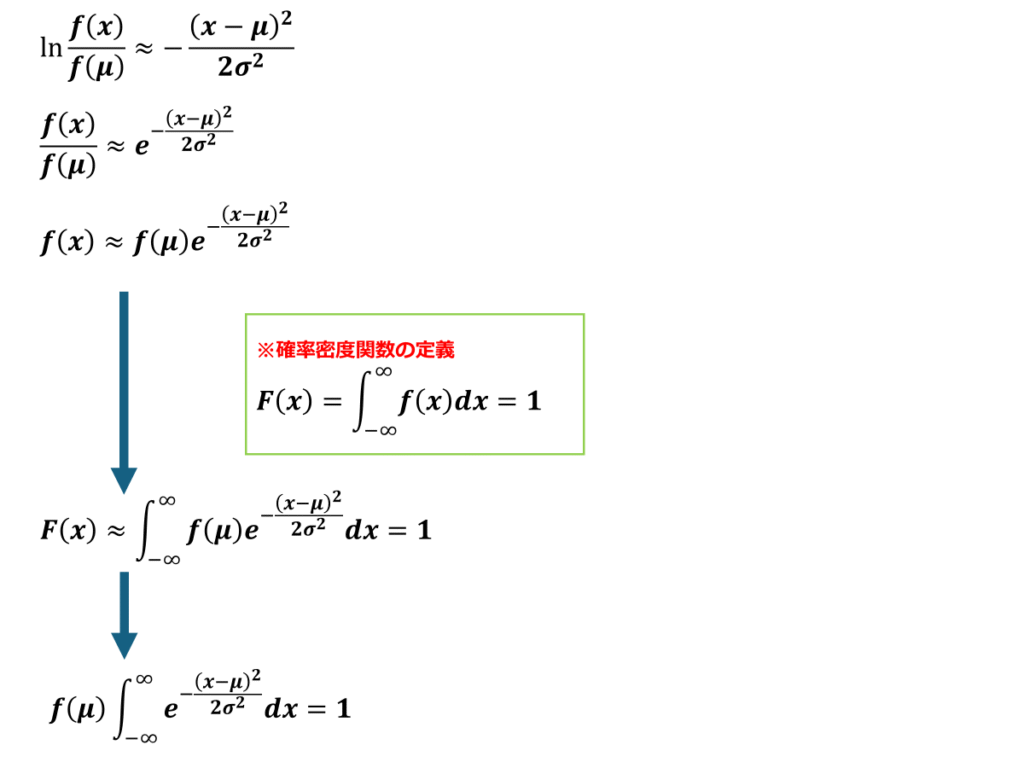
計算過程は以下に続きます。
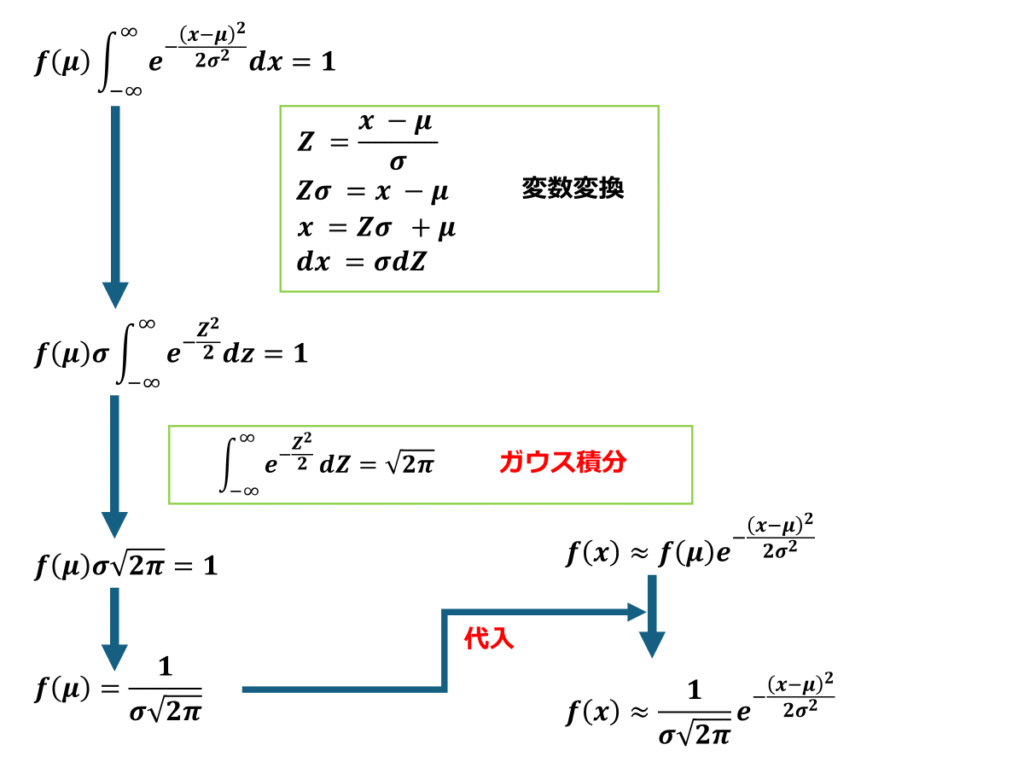
二項分布の期待値と分散を標準化すると?
ここまでで、Bin(n,p)→N(np,np(1-p))になる事が証明できました。これに確率変数の標準化の概念を組み合わせることで以下のような式変形ができます。

このことから、N(p,(p(1-p)/n))と考えられる
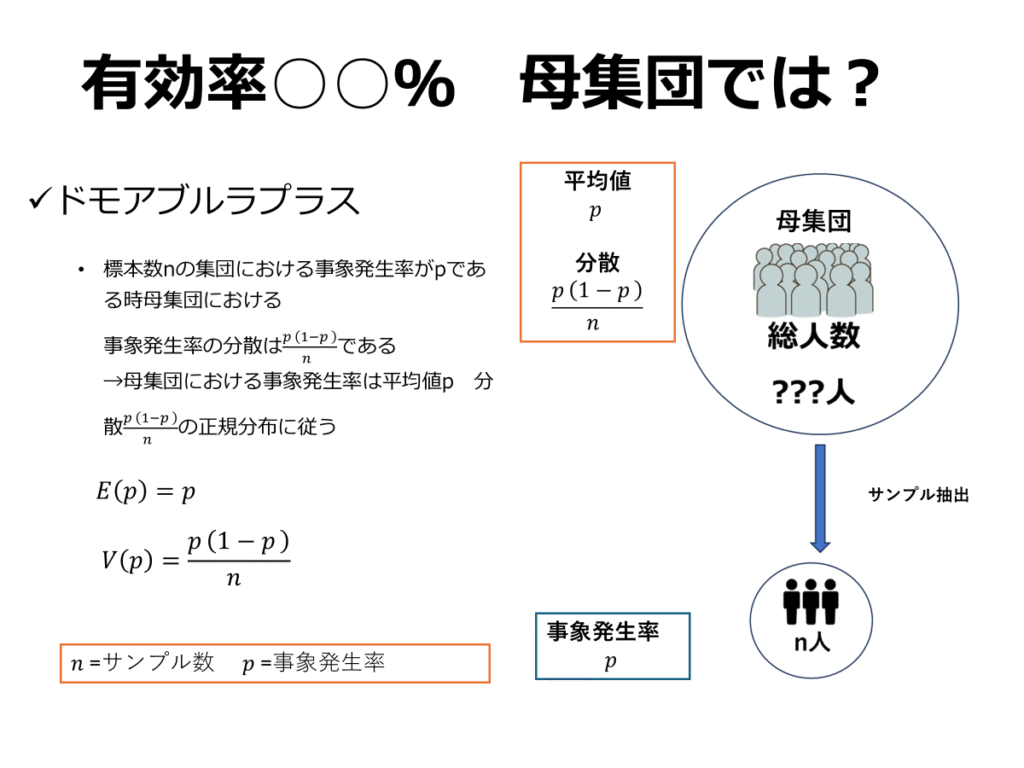
DPP4阻害薬の発生率比較に!
ここまで行った、期待値、分散の線形性、確率変数の標準化、二項分布の正規近似などを活用することで冒頭に示した以下のデータの有意差検定を実施することができます。
母集団平均が等しいと仮定した際の標準化
二項分布の期待値はnp、分散はnp(1-p)でした。また、n数が多いと二項分布は正規分布に従います。ここで確率変数xを、「n回施行した際の事象発生回数」と定義します。

上記のように式変形を行い、x/nをpの母集団推測値とします。
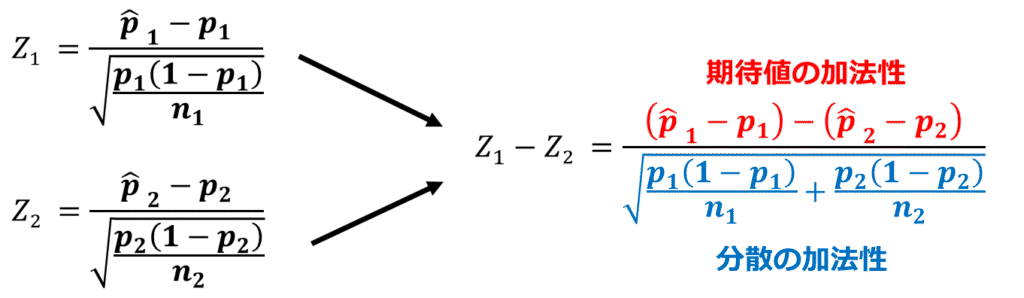
帰無仮説を、「A群とB群の母集団における事象発生確率は等しい」と置きます。そうすると推測値は同じ値になるため、式から消えます。

帰無仮説が正しいと仮定した際の標本分散の差を考えます。期待値と分散の加法性より、差の期待値を分散の和で割ることで帰無仮説が成立する場合における標準化確率変数を算出することができます。
ここで算出されたZ値が標準正規分布においてどの程度の割合で起こりうるのか?この割合をもとに帰無仮説を棄却するか判断することが統計学における「仮説検定」の考え方になります。
実際に計算をしてみると・・・
試しに以下のデータより、グリメピリド(SU尿素系薬)とリナグリプチン(DPP-4阻害薬)の間で低血糖の発生割合に差があるか?を実際に検定してみます。また、発生割合の差を疫学用語で寄与危険度と表現することもあります。

上記で導出した式をもとに実際に計算してみます。表より、リナグリプチン群(n1=1170 p1=0.0205)グリメピリド群(n2=955 ,p2=0.0408)として計算を行います。

Z値は、2.67となります。標準正規分布において、確率変数が2.67以上になる確率は0.0037となります。これは、「帰無仮説が正しいと仮定した場合、今回の結果が起こりうる確率は0.0037である」と解釈され、これは0.01を下回っています。これより、グリメピリド群とリナグリプチン群の低血糖発生率は等しいという帰無仮説は棄却されることになります。

ほかの薬についても同様に検定を行った結果上記のようになりました。リナグリプチンとグリメピリドの比較。※この二つの薬剤について
まとめ
- 期待値、分散、共分散。
- 期待値、分散の加法性と線形性。
- 確率変数の標準化。
- 二項分布の期待値と分散。
- 正規分布の期待値と分散。






コメント